
分析 (Ⅰ)由等边三角形性质得c=$\sqrt{3}$,由椭圆离心率为$\frac{\sqrt{3}}{4}$,得a=4,由此能求出曲线C的方程.
(Ⅱ)若存在这样的直线,则四边形F1AF2B是平行四边形,由对称性,过原点的直线与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}$=1的交点都符合,设这样的直线l与$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}$=1,(y≥0)交于A点,与y=$\frac{1}{4}$(x2-16)(y<0)交于B点,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}=1}\\{y=\frac{1}{4}({x}^{2}-16),(y<0)}\end{array}\right.$,得B点坐标,由此能求出结果.
解答 解:(Ⅰ)∵点F1(-c,0),F2(c,0),F(0,-3)为等边三角形的三个顶点,
∴$\sqrt{3}c=3$,解得c=$\sqrt{3}$,
∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{\sqrt{3}}{4}$,∴a=4,
∴b2=${4}^{2}-(\sqrt{3})^{2}$=13,
∵曲线C是由方程$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(y≥0)的弧线及方程
为y=$\frac{1}{4}({x}^{2}-{a}^{2})$(y<0)的弧线构成的封闭曲线,
∴曲线C的方程为:$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}=1,y≥0}\\{y=\frac{1}{4}({x}^{2}-16),y<0}\end{array}\right.$.
(Ⅱ)若存在这样的直线,则四边形F1AF2B是平行四边形,
由对称性,过原点的直线与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}$=1的交点都符合,
设这样的直线l与$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}$=1,(y≥0)交于A点,与y=$\frac{1}{4}$(x2-16)(y<0)交于B点,
则B是$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}$=1与y=$\frac{1}{4}$(x2-16),(y<0)的交点,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{13}=1}\\{y=\frac{1}{4}({x}^{2}-16),(y<0)}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-\frac{13}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=-\frac{13}{4}}\end{array}\right.$,
由图形知B(-$\sqrt{3}$,-$\frac{13}{4}$),或B($\sqrt{3},-\frac{13}{4}$)符合,
∴这样的直线的斜率为$\frac{-\frac{13}{4}}{-\sqrt{3}}$=$\frac{13}{12}\sqrt{3}$或$\frac{-\frac{13}{4}}{\sqrt{3}}$=-$\frac{13}{12}\sqrt{3}$,
∴这样的直线l存在,其斜率为$\frac{13}{12}\sqrt{3}$或-$\frac{13}{12}\sqrt{3}$.
点评 本题考查曲线方程的求法,考查满足条件的直线方程是否存在的判断与求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 在回归分析中,变量间的关系若是非确定性关系,那么因变量不能由自变量唯一确定 | |
| B. | 线性相关系数可以是正的也可以是负的 | |
| C. | 在回归分析中,如果r2=1或r=±1,说明x与y之间完全线性相关 | |
| D. | 样本相关系数r∈(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
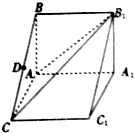 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AA1=2,AC=$\sqrt{2}$,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于E,则BE与平面ABB1A1所成角的正切值为( )
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AA1=2,AC=$\sqrt{2}$,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于E,则BE与平面ABB1A1所成角的正切值为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{10}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈N,x02≥1 | B. | ?x0∈N,x02>1 | C. | ?x∈N,x2>1 | D. | ?x∈N,x2≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com