
【题目】如图所示,三棱锥P﹣ABC中,D是AC的中点,![]() ,
,![]() ,
,![]() .
.
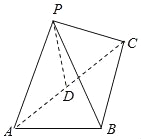
(1)求证:PD⊥平面ABC;
(2)求二面角P﹣AB﹣C的正切值大小.
【答案】(1)见解析 (2) ![]()
【解析】
(1)连接![]() ,推导出
,推导出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .(2)取
.(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() 平面
平面![]() ,从而
,从而![]() ,进而
,进而![]() 是二面角
是二面角![]() 的平面角,解三角形求得二面角
的平面角,解三角形求得二面角![]() 的正切值.
的正切值.
(1)连接BD,∵D是AC的中点,![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,即AB⊥BC.
,即AB⊥BC.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .∴PD⊥BD.
.∴PD⊥BD.
∵AC∩BD=D,∴PD⊥平面ABC.
(2)取AB的中点E,连接DE、PE,
由E为AB的中点,知DE∥BC,
∵AB⊥BC,∴AB⊥DE.∵PD⊥平面ABC,∴PD⊥AB.
又AB⊥DE,![]() ,
,
∴AB⊥平面PDE,∴PE⊥AB.
∴![]() 是二面角P﹣AB﹣C的平面角.
是二面角P﹣AB﹣C的平面角.
在△PED中,![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]() .
.
∴二面角P﹣AB﹣C的正切值为![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(x+ ![]() ),则下列结论错误的是( )
),则下列结论错误的是( )
A.f(x)的一个周期为﹣2π
B.y=f(x)的图象关于直线x= ![]() 对称
对称
C.f(x+π)的一个零点为x= ![]()
D.f(x)在( ![]() ,π)单调递减
,π)单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第![]() 天的实验需投入实验费用为
天的实验需投入实验费用为![]() 元
元![]() ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.
(1)求![]() 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;
(2)现有某知名企业对该项实验进行赞助,实验![]() 天共赞助
天共赞助![]() 元
元![]() .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求![]() 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(1)若![]() ,
,![]() ,求△
,求△![]() 的面积;
的面积;
(2)过点![]() 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求![]() ;
;
(3)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线C:y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,且A,B两点的纵坐标之积为﹣4.
(1)求抛物线C的方程;
(2)已知点D的坐标为(4,0),若过D和B两点的直线交抛物线C的准线于P点,求证:直线AP与x轴交于一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,C在圆O上,CF⊥AB于F,点D为线段CF上任意一点,延长AD交圆O于E,∠AEC=30°. 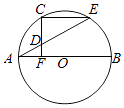
(1)求证:AF=FO;
(2)若CF= ![]() ,求ADAE的值.
,求ADAE的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为![]() .
.

(1)若E是PB的中点,求证OE∥平面PCD
(2)求侧面PAD与底面ABCD所成的二面角的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com