
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(1)若![]() ,
,![]() ,求△
,求△![]() 的面积;
的面积;
(2)过点![]() 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求![]() ;
;
(3)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
试题(1)直线AM的方程为![]() ,直线AN的方程为
,直线AN的方程为![]() ,由中位线定理知,
,由中位线定理知,![]() ,由此能求出
,由此能求出![]() 的面积.(2)由已知条件推导出
的面积.(2)由已知条件推导出![]() ,
,![]() ,由此能求出
,由此能求出![]() .(3)设直线
.(3)设直线![]() 的方程
的方程![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程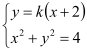 ,得
,得 同理
同理 ,由此能证明直线
,由此能证明直线![]() 过定点
过定点![]() .
.
试题解析:(1)由题知,得直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]()
所以,圆心到直线![]() 的距离
的距离![]() ,所以,
,所以,![]() ,由中位线定理知, AN=
,由中位线定理知, AN=![]() , 由题知
, 由题知![]() ,所以
,所以![]() ⊥
⊥![]() ,
,![]()
![]()
![]() =
=![]() .
.
(2)![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,
所以![]()
(3)由题知直线![]() 和直线
和直线![]() 的斜率都存在,且都不为0,不妨设直线
的斜率都存在,且都不为0,不妨设直线![]() 的的方程
的的方程![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,所以,联立方程
,所以,联立方程 ,所以,
,所以,![]() ,得
,得![]() 或
或![]() ,
,
所以![]() , 同理,
, 同理,![]() ,
,
因为![]() 轴上存在一点D
轴上存在一点D![]() ,
,
所以, =
=![]() ,同理
,同理![]() ,
,
所以,![]() =
=![]() ,所以,直线
,所以,直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】设 ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
(1)求a的值;
(2)若x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的范围.
(3)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)ex和函数g(x)=(ex﹣a)(x﹣1)2(a>0)(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)判断函数g(x)的极值点的个数,并说明理由;
(3)若函数g(x)存在极值为2a2 , 求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .现以
.现以![]() 为一边向梯形外作正方形
为一边向梯形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,如图2.
垂直,如图2.


(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,2)的直线![]() 与椭圆C:
与椭圆C:![]() 交于P,Q两点.
交于P,Q两点.
(1)若直线![]() 的斜率为k,求k的取值范围;
的斜率为k,求k的取值范围;
(2)若以PQ为直径的圆经过点E(1,0),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一般情况下,城市主干道上的车流速度 ![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 ![]() (单位:辆/千米)的函数。当主干道上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明:当
(单位:辆/千米)的函数。当主干道上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明:当 ![]() 时,车流速度
时,车流速度 ![]() 是车流密度
是车流密度 ![]() 的一次函数。
的一次函数。
(1)当 ![]() 时,求函数
时,求函数 ![]() 的表达式;
的表达式;
(2)当车流密度为多大时,车流量(单位时间内通过主干道上某观测点的车辆数,单位:辆/小时) ![]() 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com