
分析 由条件利用等差数列的定义求得C=$\frac{π}{3}$,再利用三角形的面积公式求得ab=8,再利用余弦定理,基本不等式即可求得AB边的最小值.
解答 解:△ABC中,A、C、B成等差数列,故2C=A+B,故C=$\frac{π}{3}$,A+B=$\frac{2π}{3}$.
∵△ABC的面积为$\frac{1}{2}$•ab•sinC=$\frac{1}{2}×ab×\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴ab=8,
∴AB2=c2=a2+b2-2abcosC=a2+b2-ab≥2ab-ab=ab=8,(当且仅当a=b时等号成立),
∴AB边的最小值为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查等差数列的定义,三角形的面积公式,余弦定理,基本不等式在解三角形中的应用,考查了转化思想的应用,属于基础题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
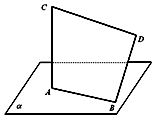 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com