
分析 以A为坐标原点,AB所在直线为x轴,AB的垂线为y轴,建立平面直角坐标系,则C(bcosA,bsinA),B(c,0),由此可证余弦定理.
解答 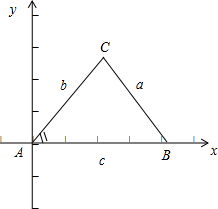 解:余弦定理:在△ABC中,设三个内角A、B、C所得边分别为a、b、c,
解:余弦定理:在△ABC中,设三个内角A、B、C所得边分别为a、b、c,
则有:a2=b2+c2-2bccosA,b2=a2+c2-2accosB,c2 =a2+b2-2abcosC.
证明:以A为坐标原点,AB所在直线为x轴,AB的垂线为y轴,建立平面直角坐标系,
则C(bcosA,bsinA),B(c,0),∴$\overrightarrow{BC}$=(c-bcosA,bsinA),
∴a2=(c-bcosA)2+(bsinA)2=b2+c2-2bccosA.
同理可证,b2=a2+c2-2accosB,c2 =a2+b2-2abcosC.
点评 本题以三角形为载体,考查学生灵活运用余弦定理化简求值,掌握余弦函数的图象和性质,是一道中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow a$•$\overrightarrow b$=0,则$\overrightarrow a$=$\overrightarrow 0$或$\overrightarrow b$=$\overrightarrow 0$ | B. | 若$\overrightarrow a$∥$\overrightarrow b$,则${\overrightarrow a^2}$•${\overrightarrow b^2}$=($\overrightarrow a$•$\overrightarrow b$)2 | ||
| C. | 若$\overrightarrow a•$$\overrightarrow c$=$\overrightarrow b$•$\overrightarrow c$,则$\overrightarrow a$=$\overrightarrow b$ | D. | 若$\overrightarrow a$∥$\overrightarrow b$,则存在实数k,使$\overrightarrow b$=k$\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
| 气温x(℃) | 18 | 15 | 11 | 9 | -3 |
| 用水量y(吨) | 69 | 57 | 45 | 47 | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com