
| A. | 若$\overrightarrow a$•$\overrightarrow b$=0,则$\overrightarrow a$=$\overrightarrow 0$或$\overrightarrow b$=$\overrightarrow 0$ | B. | 若$\overrightarrow a$∥$\overrightarrow b$,则${\overrightarrow a^2}$•${\overrightarrow b^2}$=($\overrightarrow a$•$\overrightarrow b$)2 | ||
| C. | 若$\overrightarrow a•$$\overrightarrow c$=$\overrightarrow b$•$\overrightarrow c$,则$\overrightarrow a$=$\overrightarrow b$ | D. | 若$\overrightarrow a$∥$\overrightarrow b$,则存在实数k,使$\overrightarrow b$=k$\overrightarrow a$ |
分析 利用向量的运算法则,逐一核对四个选项得答案.
解答 解:若$\overrightarrow a$•$\overrightarrow b$=0,则$\overrightarrow a$=$\overrightarrow 0$或$\overrightarrow b$=$\overrightarrow 0$或$\overrightarrow{a}⊥\overrightarrow{b}$,故A错误;
若$\overrightarrow a$∥$\overrightarrow b$,则${\overrightarrow a^2}$•${\overrightarrow b^2}$=$|\overrightarrow{a}{|}^{2}|\overrightarrow{b}{|}^{2}$,($\overrightarrow a$•$\overrightarrow b$)2=$(|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>)^{2}$
=$|\overrightarrow{a}{|}^{2}|\overrightarrow{b}{|}^{2}co{s}^{2}<\overrightarrow{a},\overrightarrow{b}>$=$|\overrightarrow{a}{|}^{2}|\overrightarrow{b}{|}^{2}$,∴则${\overrightarrow a^2}$•${\overrightarrow b^2}$=($\overrightarrow a$•$\overrightarrow b$)2,故B正确;
若$\overrightarrow{a}≠\overrightarrow{c}$,但$\overrightarrow{a}⊥\overrightarrow{b},\overrightarrow{c}⊥\overrightarrow{b}$,有$\overrightarrow a•$$\overrightarrow c$=$\overrightarrow b$•$\overrightarrow c$,故C错误;
当$\overrightarrow{a}=\overrightarrow{0}$,$\overrightarrow{b}≠\overrightarrow{0}$时,$\overrightarrow a$∥$\overrightarrow b$,此时不存在实数k,使$\overrightarrow b$=k$\overrightarrow a$,故D错误.
故选:B.
点评 本题考查平面向量的数量积运算,考查了向量垂直与数量积的关系,考查向量的运算法则,是中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
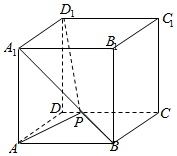 如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | 平面D1A1P⊥平面A1AP | B. | 二面角B-A1D1-A的大小为45° | ||
| C. | 三棱锥B1-D1PC的体积不变 | D. | AP+PD1的最小值为$\sqrt{2+\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=|x| | B. | f(x)=x0,g(x)=1 | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x+1}$,g(x)=x-1 | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0” | |
| B. | 若命题p:?x0∈R,x02-x0+1≤0,则¬P:?x∈R,x2-x+1>0 | |
| C. | 命题 P:若x=2且y=3,则x+y-5=0,命题P的否命题为假 | |
| D. | 设集合$A=\left\{{\left.x\right|\frac{x-1}{x+1}<0}\right\}$,B={x||x-1|<a},则“a=1”是“A∩B≠∅”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_4^4A_5^2$ | B. | $A_4^4A_3^2$ | C. | $A_4^4A_2^2$ | D. | $A_4^4A_4^1A_3^1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com