Question

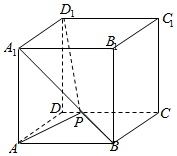
18．如图棱长为1的正方体ABCD-A₁B₁C₁D₁中，P为线段A₁B上的动点，则下列结论错误的是（　　）

• A． 平面D₁A₁P⊥平面A₁AP
• B． 二面角B-A₁D₁-A的大小为45°
• C． 三棱锥B₁-D₁PC的体积不变
• D． AP+PD₁的最小值为$\sqrt{2+\sqrt{3}}$

Answer 1

分析 利用平面D₁A₁BC，⊥平面A₁ABB₁，得出平面D₁A₁P⊥平面A₁AP，即可判断A；
由线面垂直的性质，可得A₁D₁⊥A₁A，A₁D₁⊥A₁B，则∠AA₁B为二面角B-A₁D₁-A的平面角，即可判断B；
连接AB₁，交A₁B于O，运用线面垂直的判定，可得三棱锥B₁-D₁PC的高和底面积，进而得到体积，可判断C；
将面AA₁B与面A₁BCD₁沿A₁B展成平面图形，线段AD₁即为AP+PD₁的最小值，运用余弦定理可得最小值，可判断D．

解答 解：∵平面D₁A₁P即为平面D₁A₁BC，平面A₁AP 即为平面A₁ABB₁，
而D₁A₁⊥平面A₁ABB₁，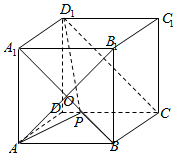
∴平面D₁A₁BC，⊥平面A₁ABB₁，∴平面D₁A₁P⊥平面A₁AP，
故A正确；
由D₁A₁⊥平面A₁ABB₁，可得A₁D₁⊥A₁A，A₁D₁⊥A₁B，
则∠AA₁B为二面角B-A₁D₁-A的平面角，且∠AA₁B=45°，
故B正确；
连接AB₁，交A₁B于O，则B₁O⊥A₁B，B₁O⊥A₁D₁，
可得B₁O⊥平面A₁BCD₁，在矩形A₁BCD₁中，△D₁PC的面积为$\frac{1}{2}$×$\sqrt{2}$×1=$\frac{\sqrt{2}}{2}$，
则三棱锥B₁-D₁PC的体积为$\frac{1}{3}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{6}$，
故C正确；
将面AA₁B与面A₁BCD₁沿A₁B展成平面图形，
线段AD₁即为AP+PD₁的最小值，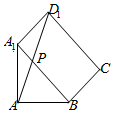

在△D₁A₁A中，∠D₁A₁A=135°，利用余弦定理解三角形得
AD₁=$\sqrt{1+1-2×1×1×（-\frac{\sqrt{2}}{2}）}$=$\sqrt{2+\sqrt{2}}$，
即AP+PD₁≥AD₁=$\sqrt{2+\sqrt{2}}$．
故D错误．
故选：D．

点评 本题考查正方体的结构特征，空间位置关系的判定和空间角的求法，注意运用转化的思想，考查空间推理和运算能力，属于中档题．