
已知函数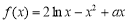 (
(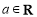 ).
).
(Ⅰ)当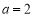 时,求
时,求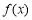 的图象在
的图象在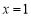 处的切线方程;
处的切线方程;
(Ⅱ)若函数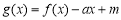 在
在 上有两个零点,求实数
上有两个零点,求实数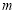 的取值范围;
的取值范围;
(Ⅲ)若函数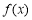 的图象与
的图象与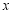 轴有两个不同的交点
轴有两个不同的交点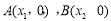 ,且
,且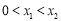 ,
,
求证: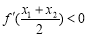 (其中
(其中 是
是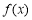 的导函数).
的导函数).
(Ⅰ) ; (Ⅱ)实数
; (Ⅱ)实数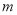 的取值范围是
的取值范围是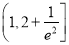 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)先求函数 的导数
的导数 ,确定切线的斜率和切点的坐标,写出切线的点斜式方程;(Ⅱ)由题设知
,确定切线的斜率和切点的坐标,写出切线的点斜式方程;(Ⅱ)由题设知 ,利用其导数研究函数
,利用其导数研究函数 在区间
在区间 上的单调性与极值和区间端点外的函数值,结合函数图象的示意图确定函数
上的单调性与极值和区间端点外的函数值,结合函数图象的示意图确定函数 在
在 上有两个零点的条件:
上有两个零点的条件:
 ,解出实数
,解出实数 的取值范围;
的取值范围;
(Ⅲ)设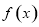 的图象与
的图象与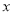 轴交于两个不同的点
轴交于两个不同的点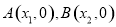 所以方程
所以方程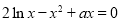 的两个根为
的两个根为 ,则
,则 ,两式相减得
,两式相减得 结合
结合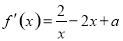
消去 可得:
可得: ,以下只需要用构造法证明
,以下只需要用构造法证明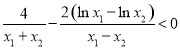 即可.
即可.
试题解析:【解析】
(Ⅰ)当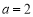 时,
时,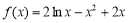 ,
,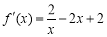 ,切点坐标为
,切点坐标为 ,
,
切线的斜率 ,则切线方程为
,则切线方程为 ,即
,即 . 2分
. 2分
(Ⅱ) ,则
,则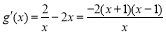 ,
,
∵ ,故
,故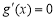 时,
时,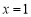 .当
.当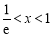 时,
时, ;当
;当 时,
时, .
.
故 在
在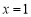 处取得极大值
处取得极大值 . 4分
. 4分
又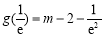 ,
, ,
,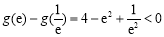 ,则
,则 ,
,
所以, 在
在 上的最小值是
上的最小值是 6分
6分
 在
在 上有两个零点的条件是
上有两个零点的条件是 ,解得
,解得
所以实数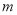 的取值范围是
的取值范围是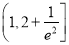 8分
8分
(Ⅲ)因为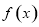 的图象与
的图象与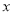 轴交于两个不同的点
轴交于两个不同的点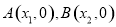
所以方程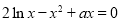 的两个根为
的两个根为 ,则
,则 ,两式相减得
,两式相减得
 ,又
,又 ,则
,则

下证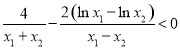 (*),即证明
(*),即证明
 即证明
即证明 在
在 上恒成立 10分
上恒成立 10分
因为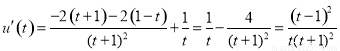 又
又 ,所以
,所以
所以, 在
在 上是增函数,则
上是增函数,则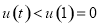 ,从而知
,从而知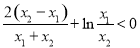
故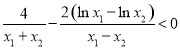 ,即
,即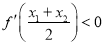 成立
成立
考点:1、导数的几何意义;2、导数在研究函数性质中的应用;3、构造法解决函数不等式的综合问题.


科目:高中数学 来源:2015届湖南省衡阳市高三上学期五校联考文科数学试卷(解析版) 题型:选择题
已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos 2A=0,a=7,c=6,则b=( )
A.10 B.9 C.8 D.5
查看答案和解析>>
科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考理科数学试卷(解析版) 题型:选择题
函数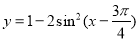 是( )
是( )
A.最小正周期为 的奇函数
的奇函数
B.最小正周期为 的偶函数
的偶函数
C.最小正周期为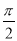 的奇函数
的奇函数
D.最小正周期为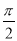 的偶函数
的偶函数
查看答案和解析>>
科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考文科数学试卷(解析版) 题型:解答题
对于函数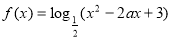 ,解答下述问题:
,解答下述问题:
(1)若函数的定义域为R,求实数a的取值范围;
(2)若函数的值域为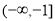 ,求实数a的值;
,求实数a的值;
查看答案和解析>>
科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考文科数学试卷(解析版) 题型:选择题
对于函数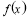 ,使
,使 成立的所有常数
成立的所有常数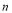 中,我们把
中,我们把 的最小值
的最小值 叫做函数
叫做函数 的上确界.
的上确界.
则函数 的上确界是( )
的上确界是( )
A.0 B. C.1 D.2
C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高三上学期第三次月考文科数学试卷(解析版) 题型:填空题
某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t =0时,点A与钟面上标12的点B重合,将A、B两点的距离d (cm)表示成t (秒)的函数,则d=______________其中 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com