
分析 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-1)n}$,再裂项,即可证明结论.
解答 证明:∵1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-1)n}$
=1+1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$=2-$\frac{1}{n}$<2,
∴1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<2.
点评 本题考查用放缩法证明不等式,掌握好放缩的程度,是解题的难点.


科目:高中数学 来源: 题型:选择题
 如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )| A. | 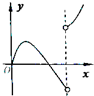 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
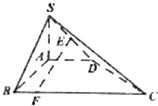 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com