
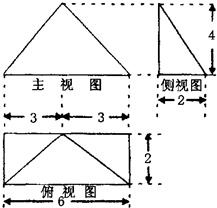
| 22+42 |
| 5 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
 (2013•江苏一模)某部门要设计一种如图所示的灯架,用来安装球心为O,半径为R(米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托
(2013•江苏一模)某部门要设计一种如图所示的灯架,用来安装球心为O,半径为R(米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托 |
| EA |
 |
| EB |
 |
| EC |
 |
| ED |
| a |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
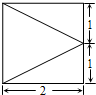 已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.查看答案和解析>>
科目:高中数学 来源:2013-2014学年北京市海淀区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.

(1)若该四棱锥的左视图为直角三角形,则它的体积为__________;
(2)关于该四棱锥的下列结论中:
①四棱锥中至少有两组侧面互相垂直;
②四棱锥的侧面中可能存在三个直角三角形;
③四棱锥中不可能存在四组互相垂直的侧面.
所有正确结论的序号是___________.
查看答案和解析>>
科目:高中数学 来源:2013年江苏省苏锡常镇、徐州、连云港六市高考数学一模试卷(解析版) 题型:解答题
 ,
, ,
, ,
,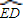 所在圆的圆心都是O、半径都是R(米)、圆弧的圆心角都是θ(弧度);灯杆EF垂直于地面,杆顶E到地面的距离为h(米),且h>R;灯脚FA1,FB1,FC1,FD1是正四棱锥F-A1B1C1D1的四条侧棱,正方形A1B1C1D1的外接圆半径为R(米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a(元),灯托造价是每米
所在圆的圆心都是O、半径都是R(米)、圆弧的圆心角都是θ(弧度);灯杆EF垂直于地面,杆顶E到地面的距离为h(米),且h>R;灯脚FA1,FB1,FC1,FD1是正四棱锥F-A1B1C1D1的四条侧棱,正方形A1B1C1D1的外接圆半径为R(米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a(元),灯托造价是每米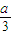 (元),其中R,h,a都为常数.设该灯架的总造价为y(元).
(元),其中R,h,a都为常数.设该灯架的总造价为y(元).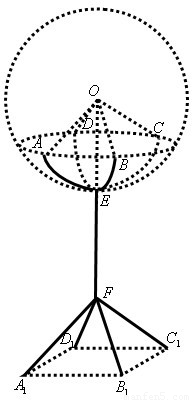
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com