
分析 利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.
解答 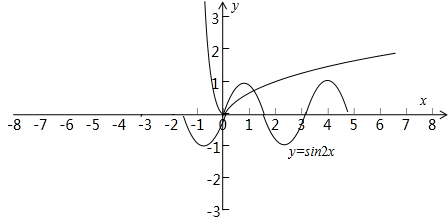 解:函数f(x)的定义域为:{x|x>-1}.
解:函数f(x)的定义域为:{x|x>-1}.
f(x)=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|
=2sinx$(2co{s}^{2}\frac{x}{2}-1)$-|ln(x+1)|
=sin2x-|ln(x+1)|,
分别画出函数y=sin2x,y=|ln(x+1)|的图象,
由函数的图象可知,交点个数为2.
所以函数的零点有2个.
故答案为:2.
点评 本题考查三角函数的化简,函数的零点个数的判断,考查数形结合与转化思想的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
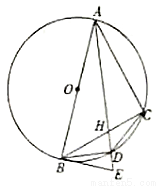
如图,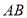 是
是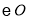 的直径,
的直径,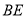 为
为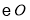 的切线,点
的切线,点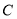 为
为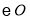 上不同于
上不同于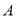 、
、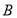 的一点,
的一点,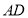 为
为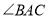 的平分线,且分别与
的平分线,且分别与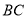 交于
交于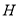 ,与
,与 交于
交于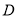 ,与
,与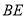 交于
交于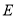 ,连接
,连接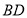 、
、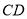 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: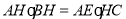 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com