
分析 由题意判断出正四面体是单位正方体的内接球的内接正四面体,画出图象再求出最小距离值.
解答 解:由题意可知,正四面体只需在单位正方体的内接球内,
即是正四面体是单位正方体的内接球的内接正四面体,如图:
先作正方体的内切球O,点H是右侧面的中心,在球O上,P为正方体的顶点,
内切球与体对角线交于点Q,此时PQ间的距离取得最小值,
因为正方体的棱长为1,则内接球的半径为$\frac{1}{2}$,
所以|PQ|=$\frac{\sqrt{3}}{2}-\frac{1}{2}$=$\frac{\sqrt{3}-1}{2}$,
故答案为:$\frac{\sqrt{3}-1}{2}$.
点评 本题考查了正方体、内接球和内接四面体的关系,考查了空间想象能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
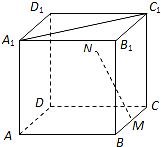 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,5) | B. | (-2,5) | C. | (5,-2) | D. | (5,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com