
(本小题满分14分)如图,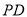 垂直于梯形
垂直于梯形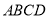 所在的平面,
所在的平面, .
.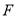 为
为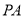 中点,
中点,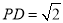 ,
,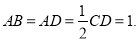 四边形
四边形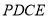 为矩形,线段
为矩形,线段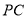 交
交 于点N .
于点N .

(1)求证: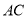 // 平面
// 平面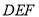 ;
;
(2)求二面角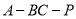 的大小;
的大小;
(3)在线段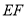 上是否存在一点
上是否存在一点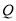 ,使得
,使得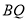 与平面
与平面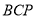 所成角的大小为
所成角的大小为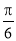 ? 若存在,请求出
? 若存在,请求出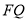 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)详见解析;(2) (3)在线段
(3)在线段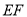 上存在一点
上存在一点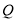 ,且
,且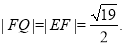
【解析】
试题分析:(1)连接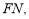 在
在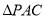 中,由题设知
中,由题设知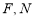 分别为
分别为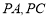 中点,所以
中点,所以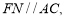 由此可证
由此可证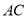 // 平面
// 平面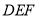 ;
;
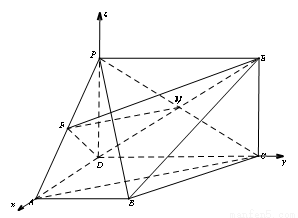
(2)如图以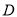 为原点,分别以
为原点,分别以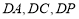 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系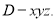 利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角
利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角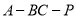 的大小;
的大小;
(3)首先假设存在点Q满足条件.由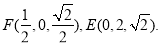 设
设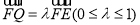 ,再利用向量的夹角公式确定
,再利用向量的夹角公式确定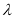 的值.
的值.
试题解析:【解析】
(Ⅰ)连接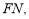 在
在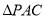 中,
中,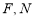 分别为
分别为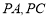 中点,所以
中点,所以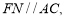
因为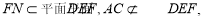
所以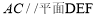 4分
4分
(2)如图以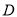 为原点,分别以
为原点,分别以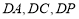 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系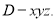 5分
5分
则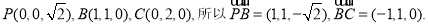
设平面 的法向量为
的法向量为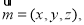 则
则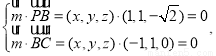
即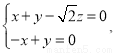 解得
解得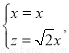
令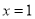 ,得
,得  所以
所以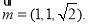 7分
7分
因为平
所以 ,
,
由图可知二面角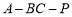 为锐二面角,
为锐二面角,
所以二面角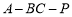 的大小为
的大小为 9分
9分
(3)设存在点Q满足条件.
由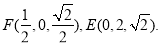 设
设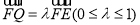 ,
,
整理得 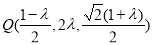 ,
, 11分
11分
因为直线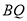 与平面
与平面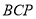 所成角的大小为
所成角的大小为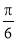 ,
,
所以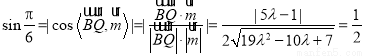 , 13分
, 13分
则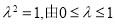 知
知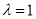 ,即
,即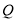 点与E点重合.
点与E点重合.
故在线段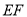 上存在一点
上存在一点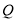 ,且
,且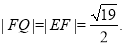 14分
14分
考点:1、空间直线与平面的位置关系;2、空间向量在解决立体几何问题中的应用.


科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试文科数学试卷(解析版) 题型:填空题
2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为 ,那么
,那么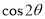 的值等于 .
的值等于 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省厦门市高三上学期期末质量检测理科数学试卷(解析版) 题型:选择题
已知l,m表示两条不同的直线, 表示平面,下列说法正确的是( ) .
表示平面,下列说法正确的是( ) .
A.若 ,则
,则 B.若
B.若 ,则
,则
C.若 ,则
,则 D.若
D.若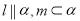 ,则
,则
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测理科数学试卷(解析版) 题型:选择题
已知直线m和平面α,β,则下列四个命题中正确的是
A.若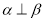 ,
, ,则
,则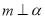
B.若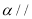
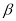 ,
,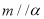 ,则
,则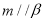
C.若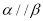 ,
,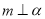 ,则
,则
D.若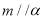 ,
,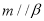 ,则
,则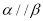
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高一上学期一模数学试卷(解析版) 题型:选择题
已知函数f(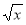 +1)=x+1,则函数f(x)的解析式为( )
+1)=x+1,则函数f(x)的解析式为( )
A.f(x)=x2 B.f(x) =x2+1(x≥1)
C.f(x)=x2-2x+2 (x≥1) D.f(x)=x2-2x(x≥1)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
已知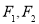 是椭圆和双曲线的公共焦点,
是椭圆和双曲线的公共焦点, 是他们的一个公共点,且
是他们的一个公共点,且 ,则椭圆和双曲线的离心率的倒数之和的最大值为
,则椭圆和双曲线的离心率的倒数之和的最大值为
A. B.
B.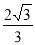 C.3 D.2
C.3 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com