
分析 先求出圆C:x2+y2-2ax+4ay+5a2-25=0的圆心C(2,-4),半径r=5,再过河卒子 同圆C(2,-4)直线l2:3x+4y-5=0的距离d=3,由此能求出圆C截直线l2:3x+4y-5=0所得的弦长.
解答 解:∵圆C:x2+y2-2ax+4ay+5a2-25=0的圆心C(a,-2a)在直线l1:x+y+2=0上,
∴a-2a+2=0,解得a=2,
∴圆C:x2+y2-2ax+4ay+5a2-25=0的圆心C(2,-4),
半径r=$\frac{1}{2}\sqrt{16+64+20}$=5,
圆心C(2,-4)直线l2:3x+4y-5=0的距离d=$\frac{|6-16-5|}{\sqrt{9+16}}$=3,
∴圆C截直线l2:3x+4y-5=0所得的弦长|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{25-9}$=8.
故答案为:8.
点评 本题考查圆截直线所得弦长的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
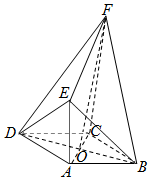 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [$\frac{π}{2}$,$\frac{5π}{6}$] | D. | [$\frac{2π}{3}$,π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 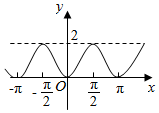 | B. | 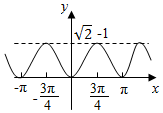 | ||
| C. | 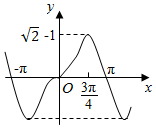 | D. | 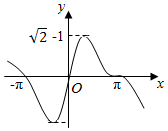 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com