Question

如图，在多面体ABCDE中，AE⊥ABC，BD∥AE，

且AC＝AB＝BC＝BD＝2，AE＝1，F在CD上（不含C, D两点）

（1）求多面体ABCDE的体积；

（2）若F为CD中点,求证：EF⊥面BCD；

 (3)当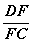的值=          时，能使AC ∥平面EFB，并给出证明。

Answer 1

解：(1)设AB中点为H，则由AC＝AB＝BC＝2，可得CH⊥AB且CH＝．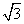

又BD∥AE，所以BD与AE共面．

又AE⊥面ABC，所以平面ABDE⊥平面ABC．

所以CH⊥平面ABDE，即CH为四棱锥C－ABDE的高．

故四棱锥C－ABDE的体积为V_C－ABDE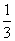＝S_ABDE·CH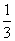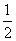＝[(1＋2)×2×]＝．

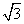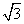(2)取BC中点G，连FG，AG．

因为AE⊥面ABC，BD∥AE，所以BD⊥面ABC．

又AGÌ面ABC，所以BD⊥AG．

又AC＝AB，G是BC的中点，所以AG⊥BC，所以AG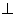平面BCD．

又因为F是CD的中点且BD＝2，所以FG∥BD且FG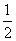＝BD＝1，所以FG∥AE．

又AE＝1，所以AE＝FG，所以四边形AEFG是平行四边形，

所以EF∥AG，所以EF⊥BCD．

（3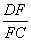）=2（证明过程略）。