
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� x��[0��1]ʱ��f��x����0.02�����ܿ�����x��1ʱ���õ�����x�ķ��̣�������ɣ�
��� �⣺x��[0��1]ʱ��f��x��=5x-2����������f��x����$\frac{1}{25}$��0.02�����ܿ�����
x��1ʱ��f��x��=$\frac{3}{5}$•${��\frac{1}{3}��}^{x}$��
��$\frac{3}{5}$•${��\frac{1}{3}��}^{x}$=0.02����ã�x��4��
��ѡ��D��
���� ���⿼���˺�����ֵ���⣬����������������ʣ���һ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
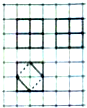 ��ͼ������ֽ��С�����εı߳�Ϊ1���������������������и���ɵļ����������ͼ����ü���������Ϊ��������
��ͼ������ֽ��С�����εı߳�Ϊ1���������������������и���ɵļ����������ͼ����ü���������Ϊ��������| A�� | $\frac{11}{2}$ | B�� | $\frac{13}{2}$ | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 1 | 2 | 3 |
| f��x�� | 2 | 3 | 1 |
| x | 1 | 2 | 3 |
| g��x�� | 3 | 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ó��������Ǽ�������� | |
| B�� | �ó���һ������ϵͳ���� | |
| C�� | �ó�����Ů�����鵽�ĸ��ʴ����������鵽�ĸ��� | |
| D�� | �ó�����Ů�����鵽�ĸ���С���������鵽�ĸ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${a_n}=-{2^{n-1}}$ | B�� | ${a_n}={2^{n-1}}$ | C�� | an=2n-3 | D�� | ${a_n}={2^{n-1}}-2$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com