
今年春节黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:性别与对景区的服务是否满意(单位:名).
| 男 | 女 | 总计 | |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(I)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?
(II)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(Ⅲ)根据以上列联表,在犯错误不超过多少的情况下认为“游客性别与对景区的服务满意”有关
|
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
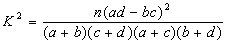 |
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了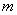 位工人某天独立生产该产品的数量,产品数量的分组区间为
位工人某天独立生产该产品的数量,产品数量的分组区间为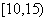 ,
,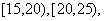

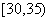 ,频率分布直方图如图所示,已知独立生产的产品数量在
,频率分布直方图如图所示,已知独立生产的产品数量在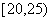 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求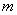 ;
;
(Ⅱ)工厂规定:若独立生产能力当日不小于25,则该工人当选今日“生产之星”.
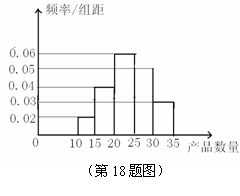 若将这天独立生产该产品数量的频率视为概率,随机从全厂工人中抽取3人,
若将这天独立生产该产品数量的频率视为概率,随机从全厂工人中抽取3人,
这3人中当日“生产之星”人数为X,求X的分布列及数学期望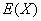 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系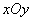 中,以坐标原点为极点,以
中,以坐标原点为极点,以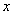 轴的非负半轴为极轴,建立极坐标系,已知直线
轴的非负半轴为极轴,建立极坐标系,已知直线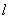 的参数方程为
的参数方程为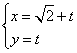 (t为参数),圆
(t为参数),圆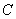 的极坐标方程是
的极坐标方程是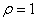 。
。
(I)求直线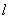 与圆
与圆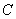 的公共点个数;
的公共点个数;
(II)在平面直角坐标系中,圆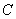 经过伸缩变换
经过伸缩变换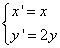 得到曲线
得到曲线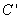 ,设
,设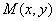 为曲线
为曲线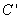 上一点,求
上一点,求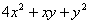 的最大值,并求相应点
的最大值,并求相应点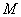 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系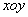 中,以坐标原点为极点,以
中,以坐标原点为极点,以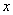 轴的非负半轴为极轴,建立极坐标系,已知直线
轴的非负半轴为极轴,建立极坐标系,已知直线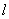 的参数方程为
的参数方程为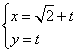 (
(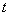 为参数),圆C的极坐标方程是
为参数),圆C的极坐标方程是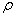 =1.
=1.
(1)求直线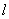 与圆
与圆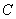 的公共点个数;
的公共点个数;
(2)在平面直角坐标系中,圆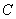 经过伸缩变换
经过伸缩变换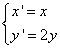 得到曲线
得到曲线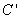 ,设
,设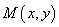 为曲线
为曲线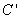 上一点,求
上一点,求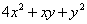 的最大值,并求相应点
的最大值,并求相应点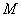 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com