
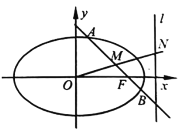
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,右准线为
,右准线为![]() .过点
.过点![]() 作与坐标轴都不垂直的直线与椭圆
作与坐标轴都不垂直的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得
,使得![]() 恒成立?若存在,求实数
恒成立?若存在,求实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),求四边形
是坐标原点),求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某总公司在A,B两地分别有甲、乙两个下属公司同时生产某种新能源产品(这两个公司每天都固定生产50件产品),所生产的产品均在本地销售.产品进入市场之前需要对产品进行性能检测,得分低于80分的定为次品,需要返厂再加工;得分不低于80分的定为正品,可以进入市场.检测员统计了甲、乙两个下属公司100天的生产情况及每件产品盈利亏损情况,数据如下表所示:
表1:
甲公司 | 得分 |
|
|
|
|
|
件数 | 10 | 10 | 40 | 40 | 50 | |
天数 | 10 | 10 | 10 | 10 | 80 |
表2:
乙公司 | 得分 |
|
|
|
| |
件数 | 10 | 5 | 40 | 45 | 50 | |
天数 | 20 | 10 | 20 | 10 | 70 |
表3:
每件正品 | 每件次品 | |
甲公司 | 盈2万元 | 亏3万元 |
乙公司 | 盈3万元 | 亏3.5万元 |
(1)分别求甲、乙两个公司这100天生产的产品的正品率(用百分数表示);
(2)试问甲乙两个公司这100天生产的产品的总利润哪个更大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
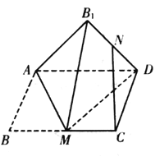
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
的中点,则在翻折过程中,下列说法中所有正确的序号是_______.
①存在某个位置,使得![]() ;
;
②翻折过程中,![]() 的长是定值;
的长是定值;
③若![]() ,则
,则![]() ;
;
④若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示
年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示![]() 月
月![]() 日至
日至![]() 月
月![]() 日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )

A.![]() 月下旬新增确诊人数呈波动下降趋势
月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,![]() 月下旬单日治愈人数超过确诊人数
月下旬单日治愈人数超过确诊人数
C.![]() 月
月![]() 日至
日至![]() 月
月![]() 日新增确诊人数波动最大
日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在![]() 月
月![]() 日左右达到峰值
日左右达到峰值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,
,![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ∥
∥![]() .判断
.判断![]() 是否为定值,若是求出该值;若不是请说明理由.
是否为定值,若是求出该值;若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com