
分析 根据题意知随机变量X的可能取值,计算对应的概率值,求出数学期望和方差.
解答 解:根据题意,摸得白球的个数为X,则X的可能取值为0,1,2;
计算P(X=0)=$\frac{4}{6}$×$\frac{3}{5}$=$\frac{2}{5}$,
p(X=1)=$\frac{4}{6}$×$\frac{2}{5}$+$\frac{2}{6}$×$\frac{4}{5}$=$\frac{8}{15}$,
p(X=2)=$\frac{2}{6}$×$\frac{1}{5}$=$\frac{1}{15}$;
∴随机变量X的数学期望为:
E(X)=0×$\frac{2}{5}$+1×$\frac{8}{15}$+2×$\frac{1}{15}$=$\frac{2}{3}$,
方差为:D(X)=${(0-\frac{2}{3})}^{2}$×$\frac{2}{5}$+${(1-\frac{2}{3})}^{2}$×$\frac{8}{15}$+${(2-\frac{2}{3})}^{2}$×$\frac{1}{15}$=$\frac{16}{45}$.
故答案为:$\frac{16}{45}$.
点评 本题考查了离散型随机变量的分布列、数学期望与方差的计算问题,是基础题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
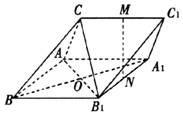 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
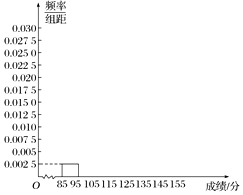 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
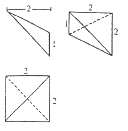 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{14}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com