练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
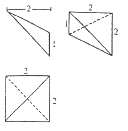
    1．已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体最长的棱长度为（　　）
    A．$2\sqrt{2}$B．$\sqrt{5}$C．3D．$2\sqrt{3}$

    分析 由三视图可知：该几何体为三棱锥P-ABC．由正方体的性质可得：这个几何体最长的棱长度为PC．

    解答 解：由三视图可知：该几何体为三棱锥P-ABC．
    由正方体的性质可得：这个几何体最长的棱长度为PC=2$\sqrt{3}$．
    故选：D．

    点评 本题考查了三棱锥与正方体的三视图、体积计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

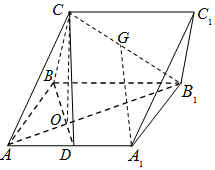    17．在三棱柱ABC-A1B1C1中，侧面ABB1A1为矩形，AB=2，AA1=2$\sqrt{2}$，D是AA1的中点，BD与AB1交于点O，且OC⊥平面ABB1A1．
    （Ⅰ）证明：平面AB1C⊥平面BCD；
    （Ⅱ）若G为B1C上的一点，A1G∥平面BCD，证明：G为B1C的中点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．一口袋中装有大小相同的2个白球和4个黑球，每次从袋中任意摸出一个球，若采取不放回抽样方式，从中摸出两个球，则摸得白球的个数X的方差D（X）=$\frac{16}{45}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知a，b，c分别为△ABC内角A，B，C的对边，$\frac{sinA}{sinC}=\frac{asinB}{a-bcosC}$．
    （Ⅰ）求角B的大小；
    （Ⅱ）若△ABC边AC上的高h=b，求$\frac{sinB}{tanA}+\frac{sinB}{tanC}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知定义在R上的奇函数f（x）满足f（x）=f（x+4）且f（3）=0，则方程f（x）=0在区间（0，10）内整数根有（　　）
    A．4个B．5个C．6个D．7个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足2sin（A-$\frac{π}{3}$）=$\sqrt{3}$，sin（B-C）=4cosBsinC，则$\frac{b}{c}$等于（　　）
    A．2$\sqrt{2}$+1B．2$\sqrt{2}$-1C．$\sqrt{6}$+1D．$\sqrt{6}$-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关，抽样调查100人，得到如下数据：
    不关注关注总计
    男生301545
    女生451055
    总计7525100
    根据表中数据，通过计算统计量K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，并参考一下临界数据：
    P（K2＞k0）0.500.400.250.150.100.050.0250.0100.0050.001
    　　k00.4550.7081.3232.0722.7063.845.0246.6357.87910.83
    若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”，则此结论出错的概率不超过（　　）
    A．0.10B．0.05C．0.025D．0.01

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．如图所示的三角形数阵叫“牛顿调和三角形”，它们是整数的倒数组成的，第n行有n个数且两端的数均为$\frac{1}{n}$（n≥2），每个数是它下一行左右相邻两数的和，如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$，$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$，$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$，…，则第6行第3个数（从左往右数）为$\frac{1}{60}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．计算：$\frac{i-2\sqrt{3}}{1+2\sqrt{3}i}$+（3+i17）-${（\frac{1+i}{\sqrt{2}}）}^{20}$=4+2i．

    查看答案和解析>>

    同步练习册答案