
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
分析 由已知函数为奇函数,求出函数的周期为4可得f(0)=0⇒f(4)=f(8)=0,由f(3)=0⇒(7)=0,又f(-3)=0⇒f(1)=f(5)=f(9)=0,从而可得结果.
解答 解:由已知可知f(3)=0,
因为f(x)是R上的奇函数,所以f(-3)=-f(3)=0,f(0)=0,
又因为函数的周期为4,即f(x+4)=f(x),
所以f(0)=f(4)=f(8)=0,f(3)=f(7)=0,f(-3)=f(1)=f(5)=f(9)=0,
所以方程f(x)=0在x∈(0,10)的根有 1,3,4,5,7,8,9,共7个.
故选:D.
点评 本题主要考查了函数的奇偶性、函数的单调性及函数周期的综合运用,解决本题的关键是熟练掌握函数的各个性质并能灵活运用性质,还要具备一定的综合论证的解题能力.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
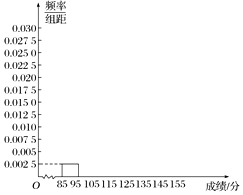 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
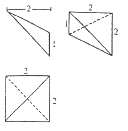 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com