
分析 利用正弦定理对△ABC三角形有解讨论.即可判断△ABC是唯一确定的锐角三角形.
解答 解:由题意,当$\sqrt{3}<a<2$时.
由正弦定理:$\frac{a}{sin60°}=\frac{2}{sinB}$
sinB=$\frac{\sqrt{3}}{a}>\frac{\sqrt{3}}{2}$,60°<B<120°,此时三角形有两个解.
当a=2时,△ABC是等边三角形.
当a>2时,B<60°;
当a>2时,且△ABC是直角三角形.a=2$\sqrt{3}$,B=30°;
综上可得:当$2≤a<2\sqrt{3}$时,此时$\frac{1}{2}<sinB=\frac{\sqrt{3}}{a}≤\frac{\sqrt{3}}{2}$唯一确定的锐角三角形,
故答案为:[2,2$\sqrt{3}$).
点评 本题考查三角形的正弦定理的运用,三角形有解情况的判断.考查运算能力,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
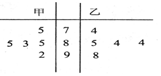 如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )| A. | x1<x2,y1<y2 | B. | x1<x2,y1>y2 | C. | x1>x2,y1>y2 | D. | x1>x2,y1<y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2≥$\frac{\sqrt{5}-1}{2}$ | B. | x1+x2<$\frac{\sqrt{5}-1}{2}$ | C. | x1+x2≥$\frac{\sqrt{5}+1}{2}$ | D. | x1+x2<$\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 不关注 | 关注 | 总计 | |
| 男生 | 30 | 15 | 45 |
| 女生 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 0.10 | B. | 0.05 | C. | 0.025 | D. | 0.01 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p<q | B. | p>q | C. | p=q | D. | 由a的取值确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com