已知圆C的圆心在直线y=4上,且过点A(4,8),B(8,4).
(1)求圆的方程;
(2)过P(8,-2)作圆的切线,求切线方程.
【答案】
分析:(1)由题意设圆心坐标为(a,4),由AC=BC可解a的值,进而可得圆的方程;
(2)设所求切线的向量为k,由圆心到直线的距离等于半径可得k的值,验证当直线的斜率不存在时也符合题意,防止漏解.
解答:解:(1)由题意设圆心坐标为(a,4),则
∵圆C过点A(4,8)和B(8,4),
∴(a-4)
2+(8-4)
2=(a-8)
2+(4-4)
2,
∴a=4,∴(a-8)
2+(4-4)
2=16
∴圆C的标准方程为:(x-4)
2+(y-4)
2=16
(2)设所求切线的向量为k,则由点斜式可得
y+2=k(x-8),即kx-y-8k-2=0,
故圆心(4,4)到直线的距离等于半径4,
即
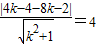
,解得k=
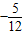
,
即切线方程为:5x+12y-16=0,
又直线无斜率时,直线方程为x=8符合题意
故所求切线的方程为:5x+12y-16=0,或x=8
点评:本题考查圆的标准方程和切线,注意当直线无斜率的情况是解决问题的关键,属中档题.

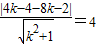 ,解得k=
,解得k=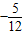 ,
,
