
分析 先求出直线的斜率,进一步求出斜率的范围,根据斜率与倾斜角的关系求出倾斜角的正切的范围,进一步求出倾斜角的范围.
解答 解:因为直线的方程为xsinθ-$\sqrt{3}$y+1=0
所以直线的斜率为k=$\frac{1}{\sqrt{3}}$sinθ,
所以-$\frac{1}{\sqrt{3}}$≤k≤$\frac{1}{\sqrt{3}}$,
设直线的倾斜角为β,则有k=tanβ,
所以-$\frac{1}{\sqrt{3}}$≤tanβ≤$\frac{1}{\sqrt{3}}$,
又因为0≤β<π,
所以0≤β≤$\frac{π}{6}$或$\frac{5π}{6}≤β<π$,即$[0,\frac{π}{6}]∪[\frac{5π}{6},π)$.
故答案为:$[0,\frac{π}{6}]∪[\frac{5π}{6},π)$.
点评 本题考查直线的倾斜角与直线的斜率的关系,注意倾斜角本身的范围在[0,π),属于基础题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{π}{2}$) | C. | (2,$\frac{4π}{3}$) | D. | (2,$\frac{7π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2f(2)>3f(3) | B. | 2f(2)<3f(3) | C. | 2f(2)=3f(3) | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
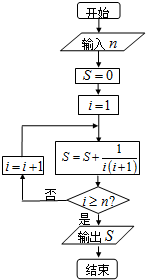
| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com