练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（x，-2），$\overrightarrow{c}$=（-1，y），若$\overrightarrow{a}$⊥$\overrightarrow{b}$且$\overrightarrow{a}$∥$\overrightarrow{c}$，则x+y=1．

    分析 利用向量垂直与数量积的关系、向量共线定理即可得出．

    解答 解：∵$\overrightarrow{a}$⊥$\overrightarrow{b}$且$\overrightarrow{a}$∥$\overrightarrow{c}$，
    ∴$\overrightarrow{a}•\overrightarrow{b}$=x-2=0，-1-y=0，
    解得x=2，y=-1．
    ∴x+y=1．
    故答案为：1．

    点评 本题考查了向量垂直与数量积的关系、向量共线定理，考查了计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

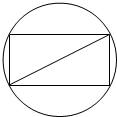    16．如图，把截面半径为10cm的圆形木头锯成矩形木料，如果矩形一边长为x，面积为y，试将y表表示成x的函数，并画出函数的大致图象，并判断怎样锯才能使得截面面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设函数f（x）=x2-3x+1，则f（a）-f（-a）=（　　）
    A．0B．-6aC．2a2+2D．2a2-6a+2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知△ABC的面积S=$\frac{\sqrt{3}}{4}$（a2+b2-c2），则角C=（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

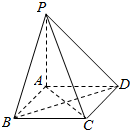    1．如图，已知四棱锥P-ABCD，ABCD为正方形，PA⊥平面ABCD，给出下列命题：
    ①PB⊥AC；
    ②平面PAB与平面PCD的交线与AB平行；
    ③平面PBD⊥平面PAC；
    ④△PBD为锐角三角形．
    其中真命题的序号是（写出全部真命题的序号）（　　）
    A．②③B．①②③④C．③④D．②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．准备一张圆形纸片，在圆内任取不同于圆心的一点F，将纸片折起，使圆周过点F（如图），然后将纸片展开，就得到一条折痕L（为了看清楚，可以把直线L画出来），这样继续下去得到若干折痕．观察这些折痕围成的轮廓，它们形成了什么曲线？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知数列{an}的前n项和为Sn，S1=2，当n≥2时，Sn=3an-2，则数列{2n-1an}的前n项和Tn=2•3n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦点为F1，F2，P为椭圆上的一点，已知$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，则△F1PF2的面积为（　　）
    A．9B．12C．10D．8

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年河北涞水波峰中学高一9月月考数学试卷（解析版） 题型：选择题

    已知函数，则（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案