
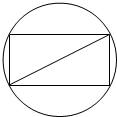
 如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大?
如图,把截面半径为10cm的圆形木头锯成矩形木料,如果矩形一边长为x,面积为y,试将y表表示成x的函数,并画出函数的大致图象,并判断怎样锯才能使得截面面积最大? 分析 首先根据矩形的一边长为xcm,表示出另外一边的长度,然后直接列出y关于x的函数.
解答  解:∵矩形的一边长为xcm,
解:∵矩形的一边长为xcm,
∴矩形的另一边长为$\sqrt{100-{x}^{2}}$cm,
∴y=x•$\sqrt{100-{x}^{2}}$,则对应的图象为:
∵直径为20cm,
∴0<x<10,
∴y=x•$\sqrt{100-{x}^{2}}$≤$\frac{{x}^{2}+100-{x}^{2}}{2}$=50,当且仅当x=$\sqrt{100-{x}^{2}}$,
即x=$\sqrt{50}$=5$\sqrt{2}$时,面积最大,最大值为50.
点评 本题考查函数模型的选择与应用,通过对实际问题的分析,抽象出数学模型,把y表示为x的函数,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 16 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com