
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,且
上一点,且![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿着
沿着![]() 折起,使点
折起,使点![]() 运动到点
运动到点![]() 处,且满足
处,且满足![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由
,由![]() ,进而
,进而![]() ,由
,由![]() ,得
,得![]() . 进而
. 进而![]() 平面
平面![]() ,进而结论可得证(2)(方法一)过
,进而结论可得证(2)(方法一)过![]() 点作
点作![]() 的平行线
的平行线![]() 交
交![]() 于点
于点![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,求得平面
,求得平面![]() 平面
平面![]() 的法向量,由二面角公式求解即可(方法二)取
的法向量,由二面角公式求解即可(方法二)取![]() 的中点
的中点![]() ,
,![]() 上的点
上的点![]() ,使
,使![]() ,连接
,连接![]() ,得
,得![]() ,
,![]() ,得二面角
,得二面角![]() 的平面角为
的平面角为![]() ,再求解即可
,再求解即可
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由已知得
,由已知得![]() ,所以
,所以![]() ,又点
,又点![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
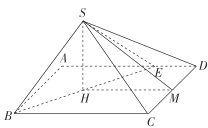
因为![]() ,点
,点![]() 是线段
是线段![]() 的中点,
的中点,
所以![]() .
.
又因为![]() ,所以
,所以![]() ,从而
,从而![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,
,![]() 不平行,
不平行,
所以![]() 平面
平面![]() .
.
(2)(方法一)由(1)知,过![]() 点作
点作![]() 的平行线
的平行线![]() 交
交![]() 于点
于点![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,则点
,则点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
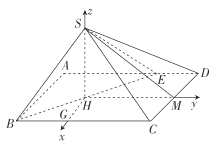
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得
,得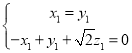 ,令
,令![]() ,得
,得![]() .
.
同理,设平面![]() 的法向量为
的法向量为![]() ,
,
由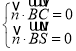 ,得
,得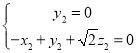 ,
,
令![]() ,得
,得![]() .
.
所以二面角![]() 的余弦值为
的余弦值为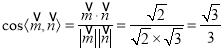 .
.
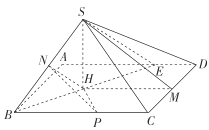
(方法二)取![]() 的中点
的中点![]() ,
,![]() 上的点
上的点![]() ,使
,使![]() ,连接
,连接![]() ,易知
,易知![]() ,
,![]() .
.
由(1)得![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以二面角![]() 的平面角为
的平面角为![]() .
.
又计算得![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD, PA=AD=2,E,F分别为PA,AB的中点,且DF⊥CE.
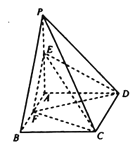
(1)求AB的长;
(2)求直线CF与平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为
的最小值为![]() ,
,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象关于原点对称.
的图象关于原点对称.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 任作一条与两条坐标轴都不垂直的直线,与椭圆
任作一条与两条坐标轴都不垂直的直线,与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8,当直线
的周长为8,当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 与
与![]() 轴垂直.
轴垂直.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,总能使
,总能使![]() 平分
平分![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
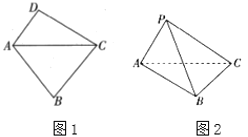
【题目】如图1,在平面四边形![]() 中,
中,![]() ,现将
,现将![]() 沿四边形
沿四边形![]() 的对角线
的对角线![]() 折起,使点
折起,使点![]() 运动到点
运动到点![]() ,如图2,这时平面
,如图2,这时平面![]() 平面
平面![]() .
.
(1)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(2)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
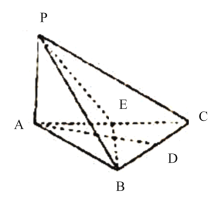
【题目】如图,三棱锥![]() 中,
中,![]() 底面
底面![]() 为等边三角形,
为等边三角形,![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)如何在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() 并说明理由;
并说明理由;
(3)若![]() ,对于(2)中的点
,对于(2)中的点![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阀值与检验》国家标准.新标准规定,车辆驾驶人员血液中的酒精含量大于或等于![]() 毫克/百毫升,小于
毫克/百毫升,小于![]() 毫克/百毫升为饮酒驾车,血液中的酒精含量大于或等于
毫克/百毫升为饮酒驾车,血液中的酒精含量大于或等于![]() 毫克/百毫升为醉酒驾车.经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下图,该函数近似模型如下:
毫克/百毫升为醉酒驾车.经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下图,该函数近似模型如下: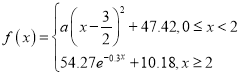 .
.
又已知刚好过1小时时测得酒精含量值为![]() 毫克/百毫升.根据上述条件,解答以下问题:
毫克/百毫升.根据上述条件,解答以下问题:
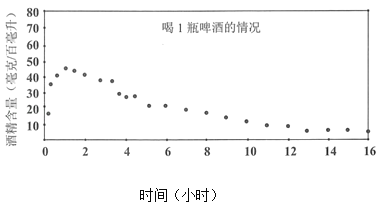
(1)试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整分钟计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com