
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪[1,+∞) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [8,+∞) | C. | (-∞,-1]∪[8,+∞) | D. | (-1,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
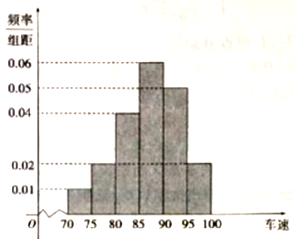 师大附中高一研究性学习小组,在某一高速公路服务区,从小型汽车中按进服务区的先后,以每间隔10辆就抽取一辆的抽样方法抽取20名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100]统计后得到如图的频率分布直方图.
师大附中高一研究性学习小组,在某一高速公路服务区,从小型汽车中按进服务区的先后,以每间隔10辆就抽取一辆的抽样方法抽取20名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100]统计后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com