
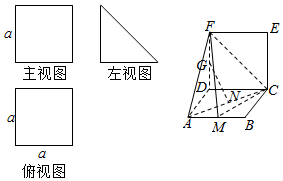
 一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.分析 (1)由棱柱的直观图和三视图可知:侧面CDFE⊥底面ABCD,四边形CDFE与ABCD都为边长为a的正方形.连接BF,BD,BD∩AC=F,可得AC⊥BD.由FD⊥DC,利用面面垂直的性质定理可得:FD⊥底面ABCD,FD⊥AC,于是AC⊥平面BDF,即可证明AC⊥GN.
(2)连接DE交FC于点O,则点O为FC的中点,取DF的中点,连接OG,AG,OM.利用三角形中位线定理与正方形的性质可得:GO$\underset{∥}{=}$AM,因此四边形AMOG是平行四边形,可得AG∥OM,再利用线面平行的判定定理即可得出.
(3)由于FD∥平面ECM.又G∈FD,因此求出点D到平面ECM的距离d即可.利用S△CDM=$\frac{1}{2}$d•CM=$\frac{1}{2}$CD2,可得d,再利用VG-ECM=$\frac{1}{3}d{S}_{△ECM}$即可得出.
解答 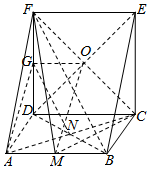 (1)证明:由棱柱的直观图和三视图可知:侧面CDFE⊥底面ABCD,四边形CDFE与ABCD都为边长为a的正方形.
(1)证明:由棱柱的直观图和三视图可知:侧面CDFE⊥底面ABCD,四边形CDFE与ABCD都为边长为a的正方形.
连接BF,BD,BD∩AC=F,可得AC⊥BD
∵FD⊥DC,侧面CDFE⊥底面ABCD,侧面CDFE∩底面ABCD=DC,
∴FD⊥底面ABCD,AC?底面ABCD,
∴FD⊥AC,
又FD∩BD=D,∴AC⊥平面BDF,GN?平面BDF.
∴AC⊥GN.
(2)解:连接DE交FC于点O,则点O为FC的中点,取DF的中点,连接OG,AG,OM.
则OG$\underset{∥}{=}$$\frac{1}{2}$DC,又AM$\underset{∥}{=}$$\frac{1}{2}$DC,
∴GO$\underset{∥}{=}$AM,
∴四边形AMOG是平行四边形,
∴AG∥OM,
又AG?平面FMC,OM?平面FMC,
∴AG∥平面FMC.
(3)解:由(1)可得:EC⊥CM.
CM=$\sqrt{{a}^{2}+(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{5}}{2}$a,∴S△ECM=$\frac{1}{2}EC•MC$=$\frac{1}{2}×a×\frac{\sqrt{5}}{2}$a=$\frac{\sqrt{5}}{4}{a}^{2}$.
∵FD∥EC,FD?平面ECM,EC?平面ECM,
∴FD∥平面ECM.
又G∈FD,因此求出点D到平面ECM的距离d即可.
由S△CDM=$\frac{1}{2}$d•CM=$\frac{1}{2}$CD2,可得:d=$\frac{{a}^{2}}{\frac{\sqrt{5}}{2}a}$=$\frac{2}{\sqrt{5}}a$.
∴VG-ECM=$\frac{1}{3}d{S}_{△ECM}$=$\frac{1}{3}×\frac{2}{\sqrt{5}}a$×$\frac{\sqrt{5}}{4}{a}^{2}$=$\frac{1}{6}{a}^{3}$.
点评 本题考查了空间位置关系、三视图、体积计算,考查了数形结合方法、推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
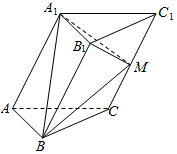 在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.
在三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,M为CC1的中点,∠ABC=90°,AC=A1A,∠A1AC=60°,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
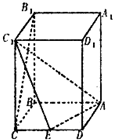 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
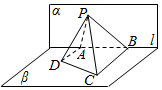 如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )
如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )| A. | 48 | B. | 16 | C. | $24\sqrt{3}$ | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com