
分析 先利用向量数量积公式确定目标函数,然后作出平面区域,根据线性规划的知识可求得z的最大值.
解答 解:z=$\overrightarrow{OA}$•$\overrightarrow{OM}$=-x+2y,
画出满足条件的平面区域,如图示:,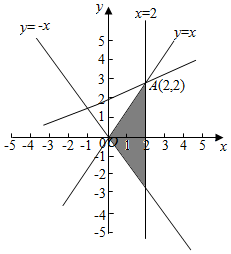
由$\left\{\begin{array}{l}{x=2}\\{x-y=0}\end{array}\right.$,解得A(2,2),
由z=-x+2y得:y=$\frac{1}{2}$x+$\frac{z}{2}$,
显然直线过A(2,2)时,z最大,
z的最大值是2,
故答案为:2.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,由平面向量数量积得到线性目标函数是关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,1] | D. | [-$\frac{1}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
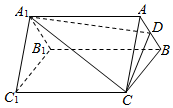 如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.
如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
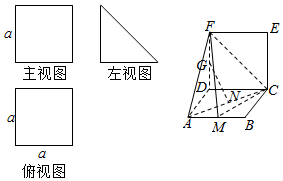 一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0,1} | D. | {-1,0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com