
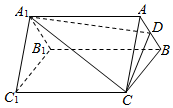
 如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.
如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5. 分析 设出棱柱的底面积和高,由D为AB的中点求出三角形ADC的面积,由棱锥体积公式求得多面体A1ADC的体积,作差得到多面体A1B1C1DBC体积,作比得答案.
解答  解:如图,设三棱柱ABC-A1BlC1的底面ABC的面积为S,高为h,
解:如图,设三棱柱ABC-A1BlC1的底面ABC的面积为S,高为h,
则三棱柱的体积V=Sh,
∵D为AB的中点,∴${S}_{△ADC}=\frac{1}{2}S$,
三棱锥A1-ADC的高为h,
∴${V}_{{A}_{1}-ADC}=\frac{1}{3}×\frac{1}{2}Sh=\frac{1}{6}Sh$,
则多面体A1B1C1DBC的体积${V}_{{A}_{1}{B}_{1}{C}_{1}DBC}=Sh-\frac{1}{6}Sh=\frac{5}{6}Sh$,
则多面体A1ADC与多面体A1B1C1DBC体积的比值为$\frac{\frac{1}{6}Sh}{\frac{5}{6}Sh}=\frac{1}{5}$.
故答案为:1:5.
点评 本题考查棱柱、棱锥、棱台的体积,考查数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
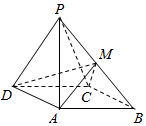 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
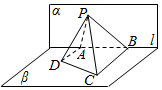 如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )
如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )| A. | 48 | B. | 16 | C. | $24\sqrt{3}$ | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com