
分析 由A,C,D三点共线可得$\overrightarrow{AC}$与$\overrightarrow{CD}$共线,由向量共线的坐标表示可得m的方程,解方程可得.
解答 解:∵向量$\overrightarrow{AB}$=(2,6),$\overrightarrow{BC}$=(-1,m),$\overrightarrow{CD}$=(3,m),
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=(2,6)+(-1,m)=(1,6+m),
∵A,C,D三点共线,∴$\overrightarrow{AC}$与$\overrightarrow{CD}$共线,
∴1×m=3(6+m)解得m=-9,
故答案为:-9.
点评 本题考查平面向量共线的坐标表示,把三点共线转化为向量共线是解决问题的关键,属基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,1] | D. | [-$\frac{1}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
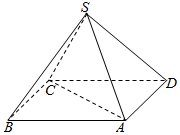 如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等
如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$或$\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{6}}{2}$或3 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{37}$+4 | B. | $\sqrt{37}$-4 | C. | $\sqrt{37}$-2$\sqrt{5}$ | D. | $\sqrt{37}$+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
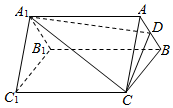 如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.
如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com