
 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.分析 (I)取OC的中点H,连接FH,BH,根据中位线定理和平行公理可知四边形BEFH是平行四边形,故EF∥BH,于是EF∥平面BOC;
(II)连结DE,OE,DG,OG,通过勾股定理计算可知DE=OE=D=OG=$\sqrt{5}$,由三线合一得出OD⊥EF,OD⊥FG,于是OD⊥平面EFG;
(III)根据中位线定理计算EG,得出△EFG是边长为$\sqrt{5}$的正三角形,以△EFG为棱锥的底面,则OF为棱锥的高,代入棱锥的体积公式计算.
解答 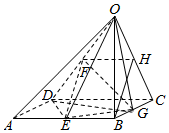 (Ⅰ)证明:取OC的中点H,连接FH,BH,
(Ⅰ)证明:取OC的中点H,连接FH,BH,
∵F,H分别是OD,OC的中点,
∴FH$\underline{\underline{∥}}$$\frac{1}{2}CD$,
又∵在正方形ABCD中,E是AB的中点,
∴EB$\underline{\underline{∥}}$$\frac{1}{2}CD$,
∴EB$\underline{\underline{∥}}$FH,
∴四边形BEFH是平行四边形,
∴EF∥BH,又∵EF?平面BOC,BH?平面BOC,
∴EF∥平面BOC.
(Ⅱ)证明:连结DE,OE,
∵四边形ABCD是边长为2的正方形,E是AB的中点,
∴$DE=\sqrt{5}$
∵侧棱OB⊥底面ABCD,AB?面ABCD,
∴OB⊥AB
又∵OB=2,EB=1,∴$OE=\sqrt{5}$,
∴$DE=OE=\sqrt{5}$,∴△ODE是等腰三角形,
∵F是OD的中点,∴EF⊥OD.
同理DG=OG=$\sqrt{5}$,∴△ODG是等腰三角形,
∵F是OD的中点,∴FG⊥OD.
又∵EF∩FG=F,EF?平面EFG,FG?面EFG,
∴OD⊥平面EFG.
(Ⅲ)解:∵侧棱OB⊥底面ABCD,BD?面ABCD,
∴OB⊥BD,
∵四边形ABCD是边长为2的正方形,
∴BD=2$\sqrt{2}$,∴OD=$\sqrt{O{B}^{2}+B{D}^{2}}$=2$\sqrt{3}$.
∵F分别是OD的中点,∴$OF=\sqrt{3}$,
∵$DE=OE=\sqrt{5}$,EF⊥OD,$DG=DG=\sqrt{5}$,FH⊥OD,
∴$EF=\sqrt{2}$,$FG=\sqrt{2}$,
∵四边形ABCD是边长为2的正方形,E,G是AB,BC的中点,
∴EG=$\frac{1}{2}AC$=$\sqrt{2}$,
∴三角形EFG是等边三角形,∴${S_{△EFG}}=\frac{{\sqrt{3}}}{2}$,
∴VG-OEF=VO-EFG=$\frac{1}{3}{S}_{△EFG}•OF$=$\frac{1}{3}×\frac{\sqrt{3}}{2}×\sqrt{3}$=$\frac{1}{2}$.
点评 本题考查了线面平行与垂直的判定,棱锥的体积计算,根据线段的长度得出线段的位置关系是解题关键.属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
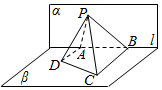 如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )
如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )| A. | 48 | B. | 16 | C. | $24\sqrt{3}$ | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
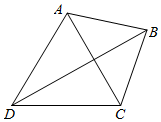 某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)
某学习小组进行课外研究性学习,为了测量如图所示不能到达的A、B两地,他们测得C、D两地的直线距离为2km,并用仪器测得相关角度大小分别为∠ADB=30°,∠CDB=30°,∠ACD=60°,∠ACB=45°,则A、B两地的距离大约等于( )(提供数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$,结果保留两个有效数字)| A. | 1.3 | B. | 1.4 | C. | 1.5 | D. | 1.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com