
分析 根据题意,作出如图的图象.由图象知,此曲线所围的力图形由一个边长为2$\sqrt{2}$的正方形与四个半径为$\sqrt{2}$的半圆组成,由此其面积易求.
解答 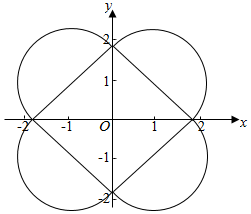 解:由题意,作出如图的图形,由曲线关于原点对称,
解:由题意,作出如图的图形,由曲线关于原点对称,
当x≥0,y≥0时,解析式为(x-1)2+(y-1)2=2,
故可得此曲线所围的力图形由一个边长为2的正方形与四个半径为$\sqrt{2}$的半圆组成,
所围成的面积是2$\sqrt{2}$×2$\sqrt{2}$+4×$\frac{1}{2}$×π×($\sqrt{2}$)2=8+4π
故答案为:8+4π.
点评 本题考查圆方程的综合应用,解题的关键是根据所给的方程,结合圆的方程的几何意义,得出方程对应的曲线形状,由图形得出解决问题的方法,本题是一个以形助数的典型题,易因为对曲线所对应的图形开关理解不准确而导致错误,或者无法下手.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
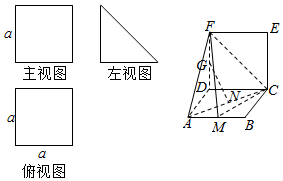 一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 昼夜温差(.C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0,1} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com