
分析 分析法证明不等式,寻找使$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b)成立的充分条件,直到使不等式成立的条件显然具备为止.
解答 证明:要证$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b),
a+b≤0,显然成立,
a+b>0时,只要证a2+b2≥$\frac{1}{2}$(a+b)2,
只要证2(a2+b2)≥a2+2ab+b2,
只要证(a-b)2≥0,
显然成立,故要证的不等式成立.
点评 本题考查不等式的证明,着重考查分析法的应用,考查推理能力,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
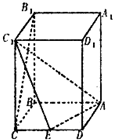 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
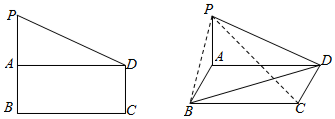 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac<bc | B. | a-b>0 | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com