
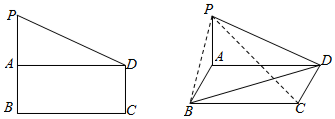
 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:分析 (1)取PA的中点E,连结OE,BE,则∠BOP为PC,BD所成的角,由PA⊥AB,PA⊥AD可得PA⊥平面ABCD,利用勾股定理求出△OBE的三边长,使用余弦定理求出cos∠BOP;
(2)P到平面ABCD的距离为PAsinθ=sinθ,代入棱锥P-ABD的体积公式求出sinθ得出θ的值.
解答 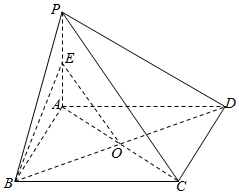 解:(1)∵AB∥CD,AB=CD,CD⊥BC,
解:(1)∵AB∥CD,AB=CD,CD⊥BC,
∴四边形ABCD是矩形,
连结AC交BD与O,则O是AC,BD的中点,
取PA的中点E,连结OE,BE,
则OE是△PAC的中位线,∴PC∥OE,OE=$\frac{1}{2}$PC.
∴∠BOE是异面直线PC,BD所成的角
∵PA⊥AB,PA⊥AD,AB∩AD=A,
∴PA⊥平面ABCD,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}=\frac{\sqrt{5}}{2}$,OB=OA=$\frac{1}{2}$BD=$\frac{1}{2}$$\sqrt{A{B}^{2}+A{D}^{2}}=\frac{\sqrt{5}}{2}$.OE=$\sqrt{A{E}^{2}+O{A}^{2}}$=$\frac{\sqrt{6}}{2}$.
∴cos∠BOE=$\frac{O{B}^{2}+O{E}^{2}-B{E}^{2}}{2OB•OE}$=$\frac{\frac{5}{4}+\frac{6}{4}-\frac{5}{4}}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{30}}{10}$.
∴∠BOE=arccos$\frac{\sqrt{30}}{10}$.即异面直线PC与BD所成的角为arccos$\frac{\sqrt{30}}{10}$.
(2)P到平面ABCD的距离h=PAsinθ=sinθ.
S△ABD=$\frac{1}{2}AB×AD$=1,
∴VP-ABD=$\frac{1}{3}{S}_{△ABD}•h$=$\frac{1}{3}×1×sinθ$=$\frac{\sqrt{2}}{6}$.
∴sinθ=$\frac{\sqrt{2}}{2}$.
∴θ=$\frac{π}{4}$或$\frac{3π}{4}$.
点评 本题考查了异面直线所成角的计算,棱锥的体积计算,作出空间角是解题关键,也可使用向量法求出,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
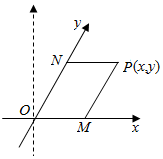 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 昼夜温差(.C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,且底面ABCD是边长为1的正方形,侧棱SA=4,AC与BD相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com