НтЃКЃЈ1ЃЉ
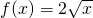
ЃЈxЁн0ЃЉ?
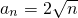
ЃЈnЮЊе§ећЪ§ЃЉЃЌ
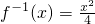
ЃЈxЁн0ЃЉ
ЫљвдЪ§Са{a
n}ЕФЗДЪ§Са{b
n}ЕФЭЈЯю
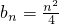
ЃЈnЮЊе§ећЪ§ЃЉЃЎ
ЃЈ2ЃЉc
n=3
nЃЌd
n=log
3nЃЌ
3
p=log
3qЃЌ
дђ
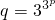
ЃЌ
га{c
n}?{d
n}ЃЌt
n=3
nЃЌ
Ыљвд{t
n}ЕФЧАnЯюКЭ
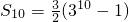
ЃЎ
ЃЈ3ЃЉЖдгкЃЈ1ЃЉжа{b
n}ЃЌ
ВЛЕШЪНЛЏЮЊЃК
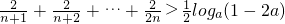
ЃЌ
ЖдШЮвте§ећЪ§nКуГЩСЂЃЌ
ЩшT
n=
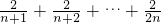
ЃЌ
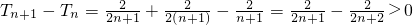
ЃЌ
Ъ§Са{T
n}ЕЅЕїЕндіЃЌ
ЫљвдЃЈT
nЃЉ
min=T
1=1ЃЌ
вЊЪЙВЛЕШЪНКуГЩСЂЃЌ
жЛвЊ
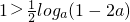
ЃЎ
Ёп1-2aЃО0ЃЌЁр

ЃЌ
1-2aЃОa
2ЃЌ
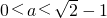
ЃЎ
ЫљвдЃЌЪЙВЛЕШЪНЖдгкШЮвте§ећЪ§КуГЩСЂЕФaЕФШЁжЕЗЖЮЇЪЧЃК
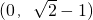
ЗжЮіЃКЃЈ1ЃЉгЩ
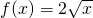
ЃЈxЁн0ЃЉЃЌжЊ
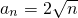
ЃЈnЮЊе§ећЪ§ЃЉЃЌ
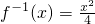
ЃЈxЁн0ЃЉЃЌгЩДЫФмЧѓГіЪ§Са{a
n}ЕФЗДЪ§Са{b
n}ЕФЭЈЯюЃЎ
ЃЈ2ЃЉгЩc
n=3
nЃЌd
n=log
3nЃЌжЊ3
p=log
3qЃЌЫљвдt
n=3
nЃЌгЩДЫФмЧѓГі{t
n}ЕФЧАnЯюКЭЃЎ
ЃЈ3ЃЉгЩ
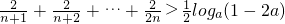
ЖдШЮвте§ећЪ§nКуГЩСЂЃЌЩшT
n=
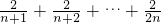
ЃЌ
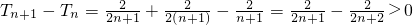
ЃЌЪ§Са{T
n}ЕЅЕїЕндіЃЌЫљвдЃЈT
nЃЉ
min=T
1=1ЃЌвЊЪЙВЛЕШЪНКуГЩСЂЃЌжЛвЊ
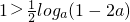
ЃЎгЩДЫФмЧѓГіЪЙВЛЕШЪНЖдгкШЮвте§ећЪ§КуГЩСЂЕФaЕФШЁжЕЗЖЮЇЃЎ
ЕуЦРЃКБОЬтПМВщЪ§СаКЭВЛЕШЪНЕФзлКЯдЫгУЃЌНтЬтЪБвЊШЯецЩѓЬтЃЌзЂвтЭкОђЬтЩшжаЕФвўКЌЬѕМўЃЌКЯРэЕиНјааЕШМлзЊЛЏЃЎ

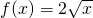 ШЗЖЈЪ§Са{an}ЕФЗДЪ§СаЮЊ{bn}ЃЌЧѓbnЃЛ
ШЗЖЈЪ§Са{an}ЕФЗДЪ§СаЮЊ{bn}ЃЌЧѓbnЃЛ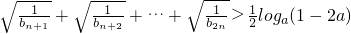 ЖдШЮвтЕФе§ећЪ§nКуГЩСЂЃЌЧѓЪЕЪ§aЕФЗЖЮЇЃЎ
ЖдШЮвтЕФе§ећЪ§nКуГЩСЂЃЌЧѓЪЕЪ§aЕФЗЖЮЇЃЎ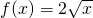 ЃЈxЁн0ЃЉ?
ЃЈxЁн0ЃЉ?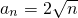 ЃЈnЮЊе§ећЪ§ЃЉЃЌ
ЃЈnЮЊе§ећЪ§ЃЉЃЌ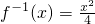 ЃЈxЁн0ЃЉ
ЃЈxЁн0ЃЉ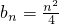 ЃЈnЮЊе§ећЪ§ЃЉЃЎ
ЃЈnЮЊе§ећЪ§ЃЉЃЎ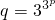 ЃЌ
ЃЌ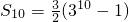 ЃЎ
ЃЎ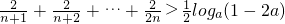 ЃЌ
ЃЌ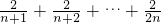 ЃЌ
ЃЌ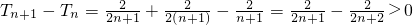 ЃЌ
ЃЌ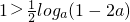 ЃЎ
ЃЎ ЃЌ
ЃЌ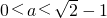 ЃЎ
ЃЎ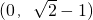
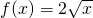 ЃЈxЁн0ЃЉЃЌжЊ
ЃЈxЁн0ЃЉЃЌжЊ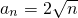 ЃЈnЮЊе§ећЪ§ЃЉЃЌ
ЃЈnЮЊе§ећЪ§ЃЉЃЌ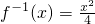 ЃЈxЁн0ЃЉЃЌгЩДЫФмЧѓГіЪ§Са{an}ЕФЗДЪ§Са{bn}ЕФЭЈЯюЃЎ
ЃЈxЁн0ЃЉЃЌгЩДЫФмЧѓГіЪ§Са{an}ЕФЗДЪ§Са{bn}ЕФЭЈЯюЃЎ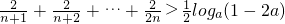 ЖдШЮвте§ећЪ§nКуГЩСЂЃЌЩшTn=
ЖдШЮвте§ећЪ§nКуГЩСЂЃЌЩшTn=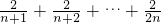 ЃЌ
ЃЌ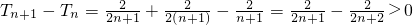 ЃЌЪ§Са{Tn}ЕЅЕїЕндіЃЌЫљвдЃЈTnЃЉmin=T1=1ЃЌвЊЪЙВЛЕШЪНКуГЩСЂЃЌжЛвЊ
ЃЌЪ§Са{Tn}ЕЅЕїЕндіЃЌЫљвдЃЈTnЃЉmin=T1=1ЃЌвЊЪЙВЛЕШЪНКуГЩСЂЃЌжЛвЊ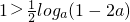 ЃЎгЩДЫФмЧѓГіЪЙВЛЕШЪНЖдгкШЮвте§ећЪ§КуГЩСЂЕФaЕФШЁжЕЗЖЮЇЃЎ
ЃЎгЩДЫФмЧѓГіЪЙВЛЕШЪНЖдгкШЮвте§ећЪ§КуГЩСЂЕФaЕФШЁжЕЗЖЮЇЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ