
【题目】对于函数![]() ,若关系式
,若关系式![]() 中变量
中变量![]() 是变量
是变量![]() 的函数,则称函数
的函数,则称函数![]() 为可变换函数.例如:对于函数
为可变换函数.例如:对于函数![]() ,若
,若![]() ,则
,则![]() ,所以变量
,所以变量![]() 是变量
是变量![]() 的函数,所以
的函数,所以![]() 是可变换函数.
是可变换函数.
(1)求证:反比例函数![]() 不是可变换函数;
不是可变换函数;
(2)试判断函数![]() 是否是可变换函数并说明理由;
是否是可变换函数并说明理由;
(3)若函数![]() 为可变换函数,求实数
为可变换函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】分析:(1)利用反证法,假设![]() 是可变换函数,
是可变换函数,![]() ,利用关变量
,利用关变量![]() 的一元二次方程无解但导出矛盾,从而可得结论;(2)利用
的一元二次方程无解但导出矛盾,从而可得结论;(2)利用![]() 必须有交点,而
必须有交点,而![]() 连续且单调递减,值域为
连续且单调递减,值域为![]() ,
,![]() 连续且单调递增,值域为
连续且单调递增,值域为![]() ,进而可得结论;. (3)
,进而可得结论;. (3)![]() ,则
,则![]() 恒大于
恒大于![]() ,即无交点,不满足题意;若
,即无交点,不满足题意;若![]() ,则
,则![]() 必定有交点,即方程
必定有交点,即方程![]() 有解,从而可得结果.
有解,从而可得结果.
详解:(1)假设![]() 是可变换函数,则
是可变换函数,则![]() ,
,
因为变量![]() 是任意的,故当
是任意的,故当![]() 时,此时有关变量
时,此时有关变量![]() 的一元二次方程无解,
的一元二次方程无解,
则与假设矛盾,故原结论正确,得证;
(2)若![]() 是可变换函数,则
是可变换函数,则![]() ,
,
则有关![]() 的两个函数:
的两个函数:![]() 必须有交点,而
必须有交点,而![]() 连续且单调递减,值域为
连续且单调递减,值域为![]() ,
,
![]() 连续且单调递增,值域为
连续且单调递增,值域为![]() ,所以这两个函数
,所以这两个函数![]() 与
与![]() 必定有交点,
必定有交点,
即:变量![]() 是变量
是变量![]() 的函数,所以
的函数,所以![]() 是可变换函数;
是可变换函数;
(3)函数![]() 为可变换函数,则
为可变换函数,则![]() ,
,
若![]() ,则
,则![]() 恒大于
恒大于![]() ,即无交点,不满足题意;
,即无交点,不满足题意;
若![]() ,则
,则![]() 必定有交点,即方程
必定有交点,即方程![]() 有解,从而满足题意.
有解,从而满足题意.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,给定数列
,给定数列![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() 为常数数列,求a的值;
为常数数列,求a的值;
(2)当![]() 时,探究
时,探究![]() 能否是等比数列?若是,求出
能否是等比数列?若是,求出![]() 的通项公式;若不是,说明理由;
的通项公式;若不是,说明理由;
(3)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,当a=1时,求证:
,当a=1时,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程![]() (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+![]() )=3
)=3![]() ,射线OM:θ=
,射线OM:θ=![]() 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为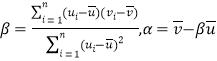 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,a为常数且a>0.
,a为常数且a>0.
(1)f(x)的图象关于直线x= ![]() 对称;
对称;
(2)若x0满足f(f(x0))=x0 , 但f(x0)≠x0 , 则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1 , x2 , 试确定a的取值范围;
(3)对于(2)中的x1 , x2 , 和a,设x3为函数f(f(x))的最大值点,A(x1 , f(f(x1))),B(x2 , f(f(x2))),C(x3 , 0),记△ABC的面积为S(a),讨论S(a)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(0,1),(3+2![]() ,0),(3-2
,0),(3-2![]() ,0)在圆C上.
,0)在圆C上.
(1)求圆C的方程.
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一微商店对某种产品每天的销售量(![]() 件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.

(1)求频率分布直方图中![]() 的值;
的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )

A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 2017年、2018年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各月仓储指数的中位数与2017年各月仓储指数中位数差异明显
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com