
分析 设直线AB方程为y=kx+m,由直线和椭圆C:$\frac{{x}^{2}}{2}$+y2=1联立,得(2k2+1)x2+4kmx+2m2-2=0,由此利用韦达定理结合已知条件能证明直线MN过定点(2,0).
解答 证明:由题意,知直线AB斜率存在,其方程为y=kx+m,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=kx+m}\end{array}\right.$,消去y,得(2k2+1)x2+4kmx+2m2-2=0,
△=(4km)2-4(2k2+1)(2m2-2)>0.
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{4km}{2{k}^{2}+1}$,x1x2=$\frac{2{m}^{2}-2}{2{k}^{2}+1}$,
且${K}_{{F}_{2}A}$=$\frac{k{x}_{1}+m}{{x}_{1}-1}$,${k}_{{F}_{2}B}=\frac{k{x}_{2}+m}{{x}_{2}-1}$,
由已知直线F2A与F2B的倾斜角互补得,
${k}_{{F}_{2}M}+{k}_{{F}_{2}N}=0$即$\frac{k{x}_{1}+m}{{x}_{1}-1}+\frac{k{x}_{2}+m}{{x}_{2}-1}=0$,
化简得,2kx1x2+(m-k)(x1+x2)-2m=0,
∴2k•$\frac{2{m}^{2}-2}{2{k}^{2}+1}$-$\frac{4km(m-k)}{2{k}^{2}+1}$-2m=0,
整理得,m=-2k,
∴直线MN的方程为y=k(x-2),
故直线MN过定点,该定点的坐标为(2,0).
点评 本题考查曲线是椭圆的证明,考查直线过定点的证明,解题时要认真审题,熟练掌握椭圆的简单性质及其应用.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
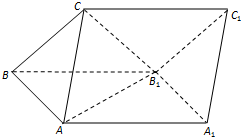 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com