
分析 求导函数,即可得函数f(x)在(0,+∞)上单调递增.先判断函数f(x)的极小值,再由函数有四个零点,进行等价转化方程有解问题,去掉绝对值,变成两个方程,即可解出b的范围.
解答 解:∵f(x)=ax+x2-xlna(a>1).
∴求导函数,可得f′(x)=axlna+2x-lna=2x+(ax-1)lna,
由于a>1,
∴lna>0,当x>0时,ax-1>0,
∴f′(x)>0,故函数f(x)在(0,+∞)上单调递增.
同理函数f(x)在(-∞,0)上单调递减,
∴f(x)min=f(0)=1,
由|f(x)-b+$\frac{1}{b}$|-3=0,
得:f(x)=b-$\frac{1}{b}$+3,或f(x)=b-$\frac{1}{b}$-3,
∵函数y=|f(x)-b+$\frac{1}{b}$|-3有四个零点,
∴$\left\{\begin{array}{l}{b-\frac{1}{b}+3>1}\\{b-\frac{1}{b}-3>1}\end{array}\right.$,
∴b-$\frac{1}{b}$>4,
解得:b>2+$\sqrt{5}$,2-$\sqrt{5}$<b<0,
∴b的范围是(2-$\sqrt{5}$,0)∪(2+$\sqrt{5}$,+∞).
点评 本题考查导数知识的运用,考查函数的单调性,考查函数的零点,考查学生分析解决问题的能力,解题的关键是利用导数确定函数的最值.


科目:高中数学 来源: 题型:解答题
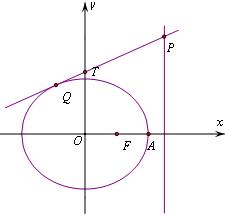 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,右焦点为F,右顶点为A,P为直线x=$\frac{5}{4}$a上的任意一点,且($\overrightarrow{PF}$+$\overrightarrow{PA}$)•$\overrightarrow{AF}$=2.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,右焦点为F,右顶点为A,P为直线x=$\frac{5}{4}$a上的任意一点,且($\overrightarrow{PF}$+$\overrightarrow{PA}$)•$\overrightarrow{AF}$=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{4}$,6) | B. | (-6,$\frac{3}{4}$) | C. | (-∞,-6)∪($\frac{3}{4}$,+∞) | D. | (-∞,-$\frac{3}{4}$)∪(6,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com