
分析 由条件、以及|xy-ab|=|y(x-a)+a(y-b)|,再利用三角不等式证得结论.
解答 证明:∵|x-a|<$\frac{?}{2}$,|y-b|<$\frac{?}{2}$,|a|≤M,|y|≤M,(M,?>0),
∴|xy-ab|=|y(x-a)+a(y-b)|≤|y(x-a)|+|a(y-b)|,
而|y(x-a)|+|a(y-b)|=|y|•|x-a|+|a|•|y-b|≤M•$\frac{?}{2}$+M•$\frac{?}{2}$=M?,
∴|xy-ab|<M?.
点评 本题主要考查绝对值三角不等式的应用,利用|xy-ab|=|y(x-a)+a(y-b)|,是证题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若{dn}满足dn=$\frac{{{b_1}+2{b_2}+3{b_3}+…+n{b_n}}}{1+2+3+…n}$,则{dn}也是等比数列 | |
| B. | 若{dn}满足dn=$\frac{{{b_1}•2{b_2}•3{b_3}•…•n{b_n}}}{1•2•3•…•n}$,则{dn}也是等比数列 | |
| C. | 若{dn}满足${d_n}={[{b_1}•(2{b_2})•(3{b_3})•…•(n{b_n})]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 | |
| D. | 若{dn}满足${d_n}={[{b_1}•{b_2}^2•{b_3}^3•…•{b_n}^n]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
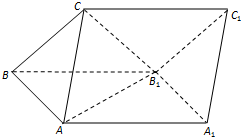 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com