
【题目】如图,一个角形海湾AOB,∠AOB=2θ(常数θ为锐角).拟用长度为l(l为常数)的围网围成一个养殖区,有以下两种方案可供选择:
方案一 如图1,围成扇形养殖区OPQ,其中![]() =l;
=l;
方案二 如图2,围成三角形养殖区OCD,其中CD=l;

(1)求方案一中养殖区的面积S1 ;
(2)求证:方案二中养殖区的最大面积S2=![]() ;
;
(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
【答案】(1)![]() (2)见解析(3)为使养殖区面积最大,应选择方案一.
(2)见解析(3)为使养殖区面积最大,应选择方案一.
【解析】分析:(1)设![]() ,利用弧长公式得
,利用弧长公式得![]() ,再利用扇形的面积公式,即可求解
,再利用扇形的面积公式,即可求解![]() ;
;
(2)设![]() ,由余弦定理和基本不等式得
,由余弦定理和基本不等式得![]() ,再利用三角形的面积公式,即可证得
,再利用三角形的面积公式,即可证得![]() ;
;
(3)由(1)(2)得![]() ,令
,令![]() ,求得
,求得![]() ,求得函数
,求得函数![]() 的单调性,得
的单调性,得![]() ,得
,得![]() ,作出相应的选择.
,作出相应的选择.
详解:解:(1)设OP=r,则l=r·2θ,即r=![]() ,
,
所以 S1=![]() lr=
lr=![]() ,θ∈(0,
,θ∈(0,![]() ).
).
(2)设OC=a,OD=b.由余弦定理,得l2=a2+b2-2abcos2θ,所以
l2≥2ab-2abcos2θ.
所以ab≤![]() ,当且仅当a=b时“=”成立.
,当且仅当a=b时“=”成立.
所以S△OCD=![]() absin2θ≤
absin2θ≤![]() =
=![]() ,即S2=
,即S2=![]() .
.
(3)![]() -
-![]() =
=![]() (tanθ-θ),θ∈(0,
(tanθ-θ),θ∈(0,![]() ),.
),.
令f(θ)=tanθ-θ,则f (θ)=(![]() )-1=
)-1=![]() .
.
当θ∈(0,![]() )时,f (θ)>0,所以f(θ)在[0,
)时,f (θ)>0,所以f(θ)在[0,![]() )上单调增,所以,当θ∈(0,
)上单调增,所以,当θ∈(0,![]() ),
),
总有f(θ)>f(0)=0.所以![]() -
-![]() >0,得S1>S2.
>0,得S1>S2.
答:为使养殖区面积最大,应选择方案一.(没有作答扣一分)


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】甲船在岛![]() 的正南方
的正南方![]() 处,
处,![]() 千米,甲船以每小时
千米,甲船以每小时![]() 千米的速度向正北航行,同时乙船自
千米的速度向正北航行,同时乙船自![]() 出发以每小时
出发以每小时![]() 千米的速度向北偏东
千米的速度向北偏东![]() 的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
A. ![]() 分钟 B.
分钟 B. ![]() 分钟 C.
分钟 C. ![]() 分钟 D.
分钟 D. ![]() 分钟
分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
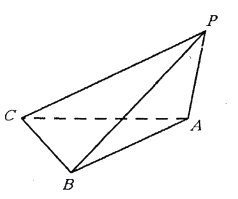
【题目】已知三棱锥 ![]() ,底面
,底面 ![]() 是以
是以 ![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() ,
, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.
(1)求直线 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(2)求二面角 ![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
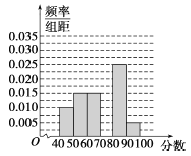
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com