
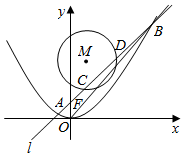
 已知抛物线C的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线C的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.分析 (1)由题意设抛物线方程为x2=2py(p>0),利用P(m,4)到焦点的距离等于P到其准线的距离,根据抛物线的定义,即可求抛物线C的方程;
(2)由于l过焦点F(0,1),所以直线l的方程为y=kx+1,与抛物线方程联立,利用韦达定理,求出|AB|,原点到直线AB的距离,即可求三角形OAB的面积.
解答 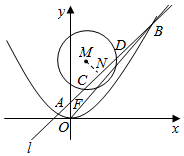 (1)解:由题意设抛物线方程为x2=2py(p>0),其准线方程为x=-$\frac{p}{2}$,
(1)解:由题意设抛物线方程为x2=2py(p>0),其准线方程为x=-$\frac{p}{2}$,
∵P(m,4)到焦点的距离等于P到其准线的距离,
∴4+$\frac{p}{2}$=5,∴p=2,
∴抛物线C的方程为x2=4y;
(2)显然直线l的斜率存在,设其斜率为k,由于l过焦点F(0,1),所以直线l的方程为y=kx+1,
取CD的中点N,连接MN,则MN⊥CD,
由于|AC|=|BD|,所以N点也是线段AB的中点,
设A(x1,y1),B(x2,y2),N(x0,y0),则x0=$\frac{{x}_{1}+{x}_{2}}{2}$,y0=$\frac{{y}_{1}+{y}_{2}}{2}$,
由$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=kx+1}\end{array}\right.$,得x2-4kx-4=0,所以x1+x2=4k,
所以x0=2k,y0=2k2+1,即N(2k,2k2+1)
又因为kMN=-$\frac{1}{k}$,即$\frac{(2{k}^{2}+1)-4}{2k-1}$=$-\frac{1}{k}$,
整理得2k3-k-1=0,即(k-1)(2k2+2k+1)=0,所以k=1
所以|AB|=y1+y2+2=(x1+1)+(x2+1)+2=8,
原点到直线AB的距离为d=$\frac{\sqrt{2}}{2}$,
所以S△OAB=$\frac{1}{2}•|AB|•d$=2$\sqrt{2}$.
点评 本题主要考查抛物线的标准方程,考查直线与抛物线的位置关系,考查韦达定理,考查学生的计算能力,属于中档题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}$) | B. | (1,$\sqrt{2}$] | C. | ($\sqrt{2}$,+∞) | D. | [$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com