
分析 (Ⅰ)利用单项式乘多项式展开,再由降幂公式和辅助角公式化积,则对称轴方程可求,由相位在正弦函数的增区间内求解x的范围得f(x)的单调增区间;
(Ⅱ)由f(A)=2求得A值,由余弦定理及基本不等式求得bc的最大值,代入三角形面积公式求得△ABC的面积的最大值.
解答 解:(Ⅰ)$f(x)=2{sin^2}x+2sinxcosx=1-cos2x+sin2x=\sqrt{2}sin(2x-\frac{π}{4})+1$,
令$sin(2x-\frac{π}{4})=\underline+1$,有$2x-\frac{π}{4}=kπ+\frac{π}{2}$,$x=\frac{kπ}{2}+\frac{3π}{8}(k∈Z)$,
∴f(x)的对称轴是$x=\frac{kπ}{2}+\frac{3π}{8}(k∈Z)$.
令$-\frac{π}{2}+2kπ≤2x-\frac{π}{4}≤\frac{π}{2}+2kπ$,得:$-\frac{π}{8}+kπ≤x≤\frac{3π}{8}+kπ,k∈Z$,
∴f(x)的递增区间是[$-\frac{π}{8}+kπ,\frac{3π}{8}+kπ$],k∈Z;
(Ⅱ)由(Ⅰ)得:$\sqrt{2}sin(2A-\frac{π}{4})+1=2$,即$sin(2A-\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,
∵A为锐角,∴$2A-\frac{π}{4}=\frac{π}{4}$,即$A=\frac{π}{4}$,
又a2=b2+c2-2bccosA,
∴$4≥2bc-\sqrt{2}bc$,即$bc≤\frac{4}{{2-\sqrt{2}}}=2(2+\sqrt{2})$,
∴${S_{△ABC}}=\frac{1}{2}bcsinA≤\frac{1}{2}×2(2+\sqrt{2})×\frac{{\sqrt{2}}}{2}=\sqrt{2}+1$,当且仅当b=c取等号,
故该三角形面积的最大值为$\sqrt{2}+1$.
点评 本题考查三角函数值的恒等变换应用,考查了正弦型函数的图象和性质,考查正弦定理和余弦定理在解三角形中的应用,是中档题.


科目:高中数学 来源: 题型:解答题
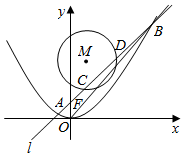 已知抛物线C的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线C的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{a^2}+{b^2}+{c^2}}$ | B. | $\sqrt{\frac{{{a^2}+{b^2}+{c^2}}}{2}}$ | C. | $\sqrt{ab+bc+ac}$ | D. | $\sqrt{\frac{3(2b+bc+ac)}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数的一条对称轴为$x=\frac{π}{6}$ | |
| B. | 函数在区间$[{\frac{π}{2},\frac{5π}{4}}]$内单调递增 | |
| C. | ?x0∈(0,3π),使f(x0)=-1 | |
| D. | ?a∈R,使得函数y=f(x+a)在其定义域内为偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有1个白球,都是白球 | B. | 恰有1个红球,恰有2个红球 | ||
| C. | 至少有1个白球,至少有1个红球 | D. | 至少有1个红球,都是白球 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年10月十八届五中全会决定全面放开二胎,这意味着一对夫妇可以生育两个孩子.全面二胎于2016年1月1日起正式实施.某地计划生育部门为了了解当地家庭对“全面二胎”的赞同程度,从当地200位城市居民中用系统抽样的方法抽取了20位居民进行问卷调查.统计如表:
2015年10月十八届五中全会决定全面放开二胎,这意味着一对夫妇可以生育两个孩子.全面二胎于2016年1月1日起正式实施.某地计划生育部门为了了解当地家庭对“全面二胎”的赞同程度,从当地200位城市居民中用系统抽样的方法抽取了20位居民进行问卷调查.统计如表:| 居民编号 | 28 | |||||||||||||||||||
| 问卷得分 | 36 | 52 | 78 | 70 | 16 | 100 | 72 | 78 | 100 | 24 | 40 | 78 | 78 | 80 | 94 | 55 | 77 | 73 | 58 | 55 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com