
设函数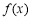 的定义域为
的定义域为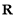 ,则“
,则“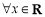 ,
, ”是“函数
”是“函数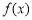 为增函数”的( )
为增函数”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源:2014-2015学年北京市西城区高三一模考试文科数学试卷(解析版) 题型:填空题
某赛事组委会要为获奖者定做某工艺品作为奖品,其中一等奖奖品3件,二等奖奖品6件. 制作一等奖和二等奖奖品所用原料完全相同,但工艺不同,故价格有所差异. 现有甲、乙两家工厂可以制作奖品(一等奖、二等奖奖品均符合要求),甲厂收费便宜,但原料有限,最多只能制作4件奖品,乙厂原料充足,但收费较贵,其具体收费情况如下表:
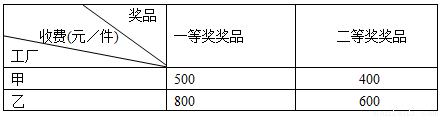
则组委会定做该工艺品的费用总和最低为 元.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三一模考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,在五面体 中,四边形
中,四边形 是边长为4的正方形,
是边长为4的正方形, ,平面
,平面
 平面
平面 ,且
,且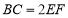 ,
,  ,点G是EF的中点.
,点G是EF的中点.

(Ⅰ)证明:
 平面
平面 ;
;
(Ⅱ)若直线BF与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的长;
的长;
(Ⅲ)判断线段 上是否存在一点
上是否存在一点 ,使
,使 //平面
//平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三一模考试理科数学试卷(解析版) 题型:填空题
已知双曲线C: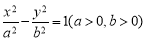 的一个焦点是抛物线
的一个焦点是抛物线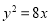 的焦点,且双曲线
的焦点,且双曲线
C的离心率为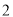 ,那么双曲线C的方程为____.
,那么双曲线C的方程为____.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三第一次综合练习文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数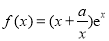 ,
,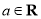 .
.
(Ⅰ)当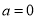 时,求曲线
时,求曲线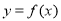 在点
在点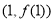 处的切线方程;
处的切线方程;
(Ⅱ)当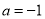 时,求证:
时,求证: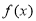 在
在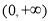 上为增函数;
上为增函数;
(Ⅲ)若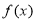 在区间
在区间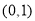 上有且只有一个极值点,求
上有且只有一个极值点,求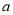 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三第一次综合练习文科数学试卷(解析版) 题型:填空题
稿酬所得以个人每次取得的收入,定额或定率减除规定费用后的余额为应纳税所得额,每次收入不超过4000元,定额减除费用800元;每次收入在4000元以上的,定率减除20%的费用.适用20%的比例税率,并按规定对应纳税额减征30%,计算公式为:
(1)每次收入不超过4000元的:应纳税额=(每次收入额-800)×20%×(1-30%)
(2)每次收入在4000元以上的:应纳税额=每次收入额×(1-20%)×20%×(1-30%).已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 元.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省皖北协作区高三3月联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)央视财经频道《升级到家》栏目答题有奖,游戏规则:每个家庭两轮游戏,均为三局两胜,第一轮3题答对2题,可获得小物件(家电),价值1600元;第二轮3题答对2题,可获得大物件(家具)价值5400元(第一轮的答题结果与第二轮答题无关),某高校大二学生吴乾是位孝顺的孩子,决定报名参赛,用自己的知识答题赢取大奖送给父母,若吴乾同学第一轮3题,每题答对的概率均为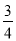 ,第二轮三题每题答对的概率均为
,第二轮三题每题答对的概率均为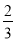 .
.
(Ⅰ)求吴乾同学能为父母赢取小物件(家电)的概率;
(Ⅱ)若吴乾同学答题获得的物品价值记为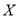 (元)求
(元)求 的概率分布列及数学期望.
的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三9月学科基础知识测试理科数学试卷(解析版) 题型:解答题
(本题15分)如图,三棱锥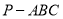 中,
中,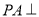 底面
底面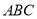 ,
,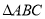 是正三角形,
是正三角形,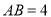 ,
, ,
,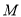 是
是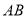 的中点.
的中点.
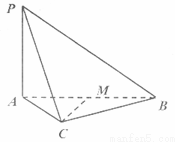
(1)求证: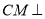 平面
平面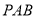 ;
;
(2)设二面角 的大小为
的大小为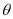 ,求
,求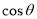 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com