
设函数f(x)=ln x-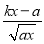 -ln a(x>0,a>0且为常数).
-ln a(x>0,a>0且为常数).
(1)当k=1时,判断函数f(x)的单调性,并加以证明;
(2)当k=0时,求证:f(x)>0对一切x>0恒成立;
(3)若k<0,且k为常数,求证:f(x)的极小值是一个与a无关的常数.
(1)见解析 (2)见解析 (3)见解析
【解析】【解析】
(1)当k=1时,
f(x)=ln x- ·x
·x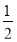 +
+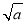 x-
x-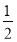 -ln a,
-ln a,
因为f′(x)=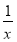 -
-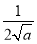 ·x-
·x-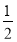 -
-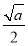 x-
x-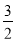
=- ≤0,
≤0,
所以函数f(x)在(0,+∞)上是单调减函数.
(2)证明:当k=0时,
f(x)=ln x+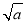 x-
x-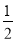 -ln a,故
-ln a,故
f′(x)=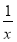 -
-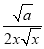 =
=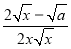 .
.
令f′(x)=0,解得x=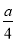 .
.
当0<x<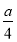 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在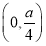 上是单调减函数;
上是单调减函数;
当x>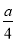 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在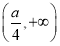 上是单调增函数.
上是单调增函数.
所以当x=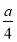 时,f′(x)有极小值,
时,f′(x)有极小值,
为f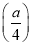 =2-2ln 2.
=2-2ln 2.
因为e>2,所以f(x)的极小值,
为f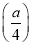 =2(1-ln 2)=2ln
=2(1-ln 2)=2ln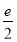 >0.
>0.
所以当k=0时,f(x)>0对一切x>0恒成立.
(3)证明:
f(x)=ln x-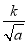 ·x
·x +
+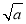 x-
x-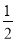 -ln a,
-ln a,
所以f′(x)=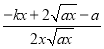 .
.
令f′(x0)=0,得kx0-2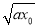 +a=0.
+a=0.
所以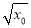 =
=
 (舍去).
(舍去).
所以x0=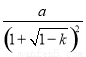 .
.
当0<x<x0时,f′(x)<0,f(x)在(0,x0)上是单调减函数;
当x>x0时,f′(x)>0,f(x)在(x0,+∞)上是单调增函数.
因此,当x=x0时,f(x)有极小值f(x0).
又f(x0)=ln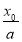 -k
-k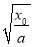 +
+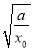 ,
,
而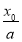 =
= 是与a无关的常数,所以ln
是与a无关的常数,所以ln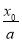 ,-k
,-k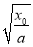 ,
,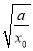 均与a无关.
均与a无关.
所以f(x0)是与a无关的常数.
故f(x)的极小值是一个与a无关的常数.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练5 函数的单调性与最值(解析版) 题型:填空题
已知函数f(x)=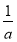 -
-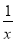 (a>0,x>0),若f(x)在
(a>0,x>0),若f(x)在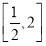 上的值域为
上的值域为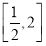 ,则a=__________.
,则a=__________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:解答题
已知f(x)是定义在集合M上的函数.若区间D⊆M,且对任意x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭.
(1)判断f(x)=x-1在区间[-2,1]上是否封闭,并说明理由;
(2)若函数g(x)=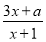 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;
(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z,且a≠b)上封闭,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:填空题
电动自行车的耗电量y与速度x之间有关系y= x3-
x3-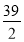 x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图像在x=1处的切线平行于直线6x+2y+5=0,则f(x)极大值与极小值之差为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:解答题
已知函数f(x)=ln x,g(x)= x2-bx(b为常数).
x2-bx(b为常数).
(1)函数f(x)的图像在点(1,f(1))处的切线与g(x)的图像相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
曲线y=x3+ax+1的一条切线方程为y=2x+1,则实数a=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
已知命题p:?a0∈R,曲线x2+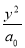 =1为双曲线;命题q:x2-7x+12<0的解集是{x|3<x<4}.给出下列结论:
=1为双曲线;命题q:x2-7x+12<0的解集是{x|3<x<4}.给出下列结论:
①命题“p∧q”是真命题;
②命题“p∧ q”是假命题;
q”是假命题;
③命题“ p∨q”是真命题;
p∨q”是真命题;
④命题“ p∨
p∨ q”是假命题.
q”是假命题.
其中正确的是________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com