
分析 (1)利用已知条件列出分段函数的解析式.
(2)利用分段函数以及函数的单调性,结合基本不等式求解函数的最值.
解答 (本小题满分14分)
解:(1)由题意,S(t)=p(t) q(t)=(140-|t-40|)(1+$\frac{{a}^{2}}{t}$)=$\left\{\begin{array}{l}{100+{a}^{2}+t+\frac{100{a}^{2}}{t},1≤t<40,t∈{N}^{•}}\\{180-{a}^{2}-t+\frac{180{a}^{2}}{t},40≤t≤60,t∈{N}^{•}}\end{array}\right.$
(2)当40≤t≤60且t∈N*时,S(t)=180-a2-t+$\frac{180{a}^{2}}{t}$,当t增加时$\frac{180{a}^{2}}{t}$减少,
所以S(t)在40≤t≤60时单调递减;当t=60时,S(t)有最小值2a2+120.
当1≤t<40且t∈N*时,S(t)=100+a2+t+$\frac{180{a}^{2}}{t}$≥100+a2+20a;
①若a=1或2或3时;当t=10a时,上述不等式中的等号成立,
S(t)在1≤t<40范围中有最小值a2+2a+100.
又在40≤t≤60时S(t)有最小值2a2+120.
当a=1时,100+a2+20a=121<122=2a2+120,故S(t)有最小值121;
当a=2或a=3时,100+a2+20a>2a2+120,故S(t)有最小值2a2+120.
②若a≥4且1≤t<40时,因为1+$\frac{100{a}^{2}}{t+1}$-$\frac{100{a}^{2}}{t}$=1-$\frac{100{a}^{2}}{t(t-1)}$≤0,
所以S(t+1)=100+a2+t+1+$\frac{100{a}^{2}}{t+1}$≤S(t)=100+a2+t+$\frac{100{a}^{2}}{t}$,
故S(t)在1≤t≤40中单调递减;又S(t)在40≤t≤60时单调递减,
所以S(t)在1≤t≤60时单调递减.
所以,当t=60时,S(t)有最小值2a2+120.
综上,若a=1,当t=10时,S(t)有最小值121;即第10天的销售额最少,为121千元.
若a≥4且a∈N*,当t=60时,S(t)有最小值2a2+120.
点评 本题考查函数的最值的求法,函数的解析式的应用,考查实际问题的解法,是中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{82}}{2}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
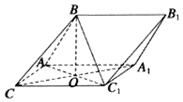 如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.
如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com