
���� ��1�����������ȥ�������ε����гɱ�����سɱ����ɣ�
��2�����û�������ʽ�ó�W�����ֵ���������ֵ���ڻ��������x������֤�����Ƿ�����������ɣ�
��3�����õ����ж�W�����ֵ�����ĵ����ԣ����ɵó�W�����ֵ������֤���ټ��ɣ�
��� �⣺��1����������һ�ε����гɱ�Ϊ$\frac{1}{1600}$��1300v2��$\frac{100}{v}$+$\frac{1}{1600}$����1300+x��v2��$\frac{100}{v}$=$\frac{1}{16}$��2600+x��v����سɱ�Ϊ10x��$\frac{100}{v}$=$\frac{1000x}{v}$��
��W=100x-$\frac{1}{16}$��2600+x��v-$\frac{1000x}{v}$��
��2����$\frac{1}{16}$��2600+x��v+$\frac{1000x}{v}$��2$\sqrt{\frac{1}{16}��2600+x��v•\frac{1000x}{v}}$=5$\sqrt{10}$•$\sqrt{��2600+x��x}$��
��W��100x-5$\sqrt{10}$•$\sqrt{��2600+x��x}$�����ҽ���$\frac{1}{16}$��2600+x��v=$\frac{1000x}{v}$��v=40$\sqrt{10}$•$\sqrt{\frac{x}{2600+x}}$ʱȡ�Ⱥţ�
��100x-5$\sqrt{10}$•$\sqrt{��2600+x��x}$��0����2$\sqrt{10x}$��$\sqrt{2600+x}$�����x��$\frac{200}{3}$��
��x=$\frac{200}{3}$ʱ��v=40$\sqrt{10}$•$\sqrt{\frac{\frac{200}{3}}{2600+\frac{200}{3}}}$=20�ʣ�0��80]��
��ÿ�����ٽ���$\frac{200}{3}$ǧ�ˣ��ſ���ʹ���ۺ������
��3���ɣ�2����֪W��100x-5$\sqrt{10}$•$\sqrt{��2600+x��x}$=5$\sqrt{10}$��2$\sqrt{10}$x-$\sqrt{x}$•$\sqrt{2600+x}$����x��[$\frac{200}{3}$��1000]��
��f��x��=2$\sqrt{10}$x-$\sqrt{x}$•$\sqrt{2600+x}$����f�䣨x��=2$\sqrt{10}$-��$\frac{1}{2\sqrt{x}}$•$\sqrt{2600+x}$+$\sqrt{x}•$$\frac{1}{2\sqrt{2600+x}}$��=2$\sqrt{10}$-$\frac{1}{2}$��$\sqrt{\frac{x+2600}{x}}$+$\sqrt{\frac{x}{x+2600}}$����
��x��[$\frac{200}{3}$��1000]����$\sqrt{\frac{x+2600}{x}}$=$\sqrt{1+\frac{2600}{x}}$��[$\sqrt{3.6}$��2$\sqrt{10}$]��
�ߺ���y=x+$\frac{1}{x}$��[$\sqrt{3.6}$��2$\sqrt{10}$]�ϵ���������
�൱$\sqrt{\frac{x+2600}{x}}$=2$\sqrt{10}$ʱ��$\sqrt{\frac{x+2600}{x}}$+$\sqrt{\frac{x}{x+2600}}$ȡ�����ֵ$\frac{41\sqrt{10}}{20}$��
��f�䣨x����2$\sqrt{10}$-$\frac{1}{2}��$$\frac{41\sqrt{10}}{20}$��0��
��f��x����[$\frac{200}{3}$��1000]�ϵ���������
�൱x=1000ʱ��f��x��ȡ�����ֵf��1000��=1400$\sqrt{10}$����ʱv=40$\sqrt{10}$•$\sqrt{\frac{1000}{1000+2600}}$=$\frac{200}{3}$�ʣ�0��80]��
��W�����ֵΪ5$\sqrt{10}$��1400$\sqrt{10}$=70000��
�൱һ�ν�����Ϊ1000ǧ�ˣ�����Ϊ$\frac{200}{3}$ǧ��/ʱʱ������ܵ����������70000Ԫ��
���� ���⿼���˺���ģ�͵�ʵ��Ӧ�ã�������ֵ�ļ����벻��ʽ��Ӧ�ã������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $-\sqrt{3}$ | C�� | $-\frac{{\sqrt{3}}}{3}$ | D�� | $\frac{{\sqrt{3}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
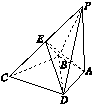 ��ͼ��ʾ��PA���ı���ABCD����ƽ�洹ֱ����PA=BC=CD=BD��AB=AD��PD��DC��
��ͼ��ʾ��PA���ı���ABCD����ƽ�洹ֱ����PA=BC=CD=BD��AB=AD��PD��DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�DΪBC���е㣬EΪAD���е㣬ֱ��BE���AC���ڵ�F����AD=BC=6����$\overrightarrow{AB}•\overrightarrow{CF}$=-18��
��ͼ���ڡ�ABC�У�DΪBC���е㣬EΪAD���е㣬ֱ��BE���AC���ڵ�F����AD=BC=6����$\overrightarrow{AB}•\overrightarrow{CF}$=-18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -6 | B�� | -1 | C�� | 1 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12�� | B�� | 16�� | C�� | 20�� | D�� | 24�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com