
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
【答案】(1)t=1;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)把A(t,1)代入y=x即可得到结论;
(2)根据题意得方程组,解方程组即可得到结论;
(3)把A(1,1)代入y=ax2+bx+4得,b=3a,继而得到对称轴为直线x=![]() ,根据1≤a≤2,得到对称轴的取值范围
,根据1≤a≤2,得到对称轴的取值范围![]() ≤x≤2,当x=
≤x≤2,当x=![]() 时,得到m=
时,得到m=![]() ,当x=2时,得到n=
,当x=2时,得到n=![]() ,即可得到结论.
,即可得到结论.
解:(1)把A(t,1)代入y=x得t=1;
(2)∵y=ax2+bx+4的图象与x轴只有一个交点,
∴![]() ,
,
∴![]() 或
或![]() ;
;
(3)把A(1,1)代入y=ax2+bx+4得,b=﹣3﹣a,
∴y=ax2﹣(a+3)x+4=a(x﹣![]() )2﹣
)2﹣![]() ,
,
∴对称轴为直线x=![]() ,
,
∵1≤a≤2,
∴![]() ≤x=
≤x=![]() ≤2,
≤2,
∵![]() ≤x≤2,
≤x≤2,
∴当x=![]() 时,y=ax2+bx+4的最大值为m=
时,y=ax2+bx+4的最大值为m=![]() ,
,
当x=2时,n=﹣![]() ,
,
∴m﹣n=![]() ,
,
∵1≤a≤2,
∴当a=2时,m﹣n的值最小,
即m﹣n的最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某射击运动员,每次击中目标的概率都是![]() .现采用随机模拟的方法估计该运动员射击
.现采用随机模拟的方法估计该运动员射击![]() 次至少击中
次至少击中![]() 次的概率:先由计算器算出
次的概率:先由计算器算出![]() 到
到![]() 之间取整数值的随机数,指定
之间取整数值的随机数,指定![]() ,
,![]() 表示没有击中目标,
表示没有击中目标,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示击中目标;因为射击
表示击中目标;因为射击![]() 次,故以每
次,故以每![]() 个随机数为一组,代表射击
个随机数为一组,代表射击![]() 次的结果.经随机模拟产生了如下
次的结果.经随机模拟产生了如下![]() 组随机数:
组随机数:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
据此估计,该射击运动员射击![]() 次至少击中
次至少击中![]() 次的概率为( )
次的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有500名职工,其中不到35岁的有125人,35-49岁的有a人,50岁及以上的有b人,现用分层抽样的方法,从中抽出100名职工了解他们的健康情况:
(1)求不到35岁的职工要抽取的人数;
(2)如果已知35-49岁的职工抽取了56人,求a的值,并求50岁及以上的职工要抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
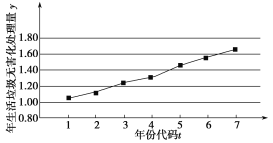
【题目】如图是我国2012年至2018年生活垃圾无害化处理量(单位:亿吨)的折线图.注:年份代码1~7分别对应年份2012~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数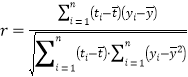 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为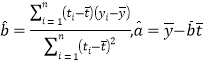 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用
的关系,可选用
A.一次函数B.二次函数
C.指数型函数D.对数型函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的椭圆
的椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() 、
、![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() ,
, ![]() ,
, ![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com