
【题目】已知过点![]() 的椭圆
的椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() 、
、![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() ,
, ![]() ,
, ![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]()
【解析】试题分析:(1)由题意,利用等差数列和椭圆的定义求出a、c的关系,再根据椭圆C过点A,求出a、b的值,即可写出椭圆C的标准方程;
(2)设P(x1,y1),Q(x2,y2),根据题意知x1=﹣2,y1=0;联立方程 消去y,由方程的根与系数关系求得x2、y2,由点A在以PQ为直径的圆外,得∠PAQ为锐角,
消去y,由方程的根与系数关系求得x2、y2,由点A在以PQ为直径的圆外,得∠PAQ为锐角, ![]()
![]() >0;由此列不等式求出k的取值范围.
>0;由此列不等式求出k的取值范围.
试题解析:
(1)∵![]() ,
, ![]() ,
, ![]() 成等差数列,
成等差数列,
∴![]() ,
,
由椭圆定义得![]() ,∴
,∴![]() ;
;
又椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,
,
∴![]() ;∴
;∴![]() ,解得
,解得![]() ,
, ![]() ;
;
∴椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)设![]() ,
, ![]() ,联立方程
,联立方程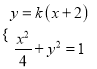 ,消去
,消去![]() 得:
得:
![]() ;
;
依题意![]() :
: ![]() 恒过点
恒过点![]() ,此点为椭圆的左顶点,∴
,此点为椭圆的左顶点,∴![]() ,
, ![]() ,①
,①
由方程的根与系数关系可得, ![]() ;②
;②
可得![]() ;③
;③
由①②③,解得![]() ,
, ![]() ;
;
由点![]() 在以
在以![]() 为直径的圆外,得
为直径的圆外,得![]() 为锐角,即
为锐角,即![]() ;
;
由![]() ,
, ![]() ,
,
∴![]() ;即
;即![]() ,
,
整理得, ![]() ,解得:
,解得: ![]() 或
或![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,给定数列
,给定数列![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() 为常数数列,求a的值;
为常数数列,求a的值;
(2)当![]() 时,探究
时,探究![]() 能否是等比数列?若是,求出
能否是等比数列?若是,求出![]() 的通项公式;若不是,说明理由;
的通项公式;若不是,说明理由;
(3)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,当a=1时,求证:
,当a=1时,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点. 
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求证:二面角C﹣PB﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题:

(1)估计这次考试的众数![]() 与中位数
与中位数![]() (结果保留一位小数);
(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知任意角
中,已知任意角![]() 以坐标原点
以坐标原点![]() 为顶点,
为顶点,![]() 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点![]() ,且
,且![]() ,定义:
,定义:![]() ,称“
,称“![]() ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数![]() ”,有同学得到以下性质:
”,有同学得到以下性质:
①该函数的值域为![]() ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;
③该函数的图象关于直线![]() 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为![]() ;
;
⑤该函数的递增区间为![]() .
.
其中正确的是__________.(填上所有正确性质的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程![]() (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+![]() )=3
)=3![]() ,射线OM:θ=
,射线OM:θ=![]() 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为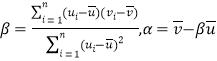 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一微商店对某种产品每天的销售量(![]() 件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.

(1)求频率分布直方图中![]() 的值;
的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com